第四十章

PBR • 理論

發布時間：2025-08-04 閱讀時間：54 分鐘

PBR，更廣為人知的名稱是「基於物理的渲染」（physically based rendering），是一系列渲染技術的集合，這些技術多多少少都基於同一套底層理論，也就是更貼近物理世界的運作方式。由於基於物理的渲染旨在以一種符合物理學原理的方式模擬光線，因此與我們最初的 Phong 和 Blinn-Phong 等照明演算法相比，它通常看起來更加真實。

PBR 不僅外觀更好，而且由於它緊密地近似了實際的物理學原理，我們（尤其是藝術家們）可以根據物理參數創作表面材質，而無需透過廉價的技巧和調整來讓光照看起來「對」。根據物理參數來創作材質的最大優勢之一是，無論光照條件如何，這些材質看起來都是正確的；這在非 PBR 的管線中是不可能實現的。

儘管如此，基於物理的渲染仍然只是對現實的一種近似（基於物理學原理），這就是為什麼它不叫「物理著色」（physical shading），而是「基於物理的著色」（physically based shading）。一個 PBR 光照模型要被認為是基於物理的，它必須滿足以下三個條件（別擔心，我們很快就會詳細介紹）：

  1. 基於微平面（microfacet）表面模型。
  2. 遵守能量守恆（energy conserving）。
  3. 使用基於物理的 BRDF。

在接下來的 PBR 章節中，我們將專注於由 Disney 最早探索，並由 Epic Games 採納用於即時顯示的 PBR 方法。他們的方法基於「金屬度工作流程」（metallic workflow），有著相當完善的文檔記錄，被大多數主流遊戲引擎廣泛採用，視覺效果也令人驚嘆。在這些章節結束時，我們將會得到一個類似下面圖片的效果：

請記住，這些章節的主題相當進階，因此建議您對 OpenGL 和著色器光照有很好的理解。您在閱讀本系列內容時，需要具備的一些較為進階的知識包括：framebuffers（幀緩衝）、cubemaps（立方體貼圖）、gamma correction（伽瑪校正）、HDR 和 normal mapping（法線貼圖）。我們還會深入探討一些進階的數學概念，但我會盡力將這些概念解釋得盡可能清楚。

微平面模型（The microfacet model）

所有的 PBR 技術都基於微平面（microfacets）理論。該理論描述了任何表面在微觀尺度下都可以由無數個微小、完美反射的鏡子所組成，這些鏡子被稱為「微平面」。根據表面的粗糙度，這些微小鏡子的排列方式會有很大的不同：

一個表面越粗糙，其微平面在表面上的排列就越混亂。這些微小鏡子排列的結果是，當我們專門討論鏡面光照/反射時，在較粗糙的表面上，射入的光線更有可能向完全不同的方向「散射」（scatter），從而產生更廣泛的鏡面反射。

相反地，在光滑的表面上，光線更有可能沿著大致相同的方向反射，這會給我們更小、更銳利的反射：

在微觀層面上，沒有任何表面是完全光滑的，但由於這些微平面小到我們無法以每個像素為基礎來區分它們，因此我們給定一個 粗糙度（roughness）參數，以統計的方式來近似表面的微平面粗糙度。

根據表面的粗糙度，我們可以計算出與某個向量 \(h\) 大致對齊的微平面的比例。這個向量 \(h\) 就是 半向量（halfway vector），它位於光線向量 \(l\) 和視角向量 \(v\) 之間的中間位置。我們在進階光照章節中已經討論過半向量，它的計算方式是將 \(l\) 和 \(v\) 的和除以其長度：

\[ h = \frac{l + v}{\|l + v\|} \]

微平面與半向量的對齊程度越高，鏡面反射就越銳利和強烈。我們可以使用一個介於 0 到 1 之間的粗糙度參數，來統計性地近似微平面的對齊情況：

我們可以看到，較高的粗糙度值會顯示出一個更大的鏡面反射形狀，這與光滑表面較小、較銳利的鏡面反射形狀形成了對比。

能量守恆（Energy conservation）

微平面近似法採用了一種形式的「能量守恆」：出射的光能絕不應超過入射的光能（不包括發光表面）。觀察上圖，我們可以看到，隨著粗糙度等級的增加，鏡面反射區域會變大，但其亮度也會隨之降低。如果每個像素的鏡面光強度都相同（無論鏡面形狀的大小），那麼較粗糙的表面將會發射出更多的能量，從而違反能量守恆原則。這就是為什麼我們在光滑的表面上看到鏡面反射更強烈，而在粗糙的表面上則顯得更微弱。

為了讓能量守恆成立，我們需要明確區分漫射光（diffuse light）和鏡面光（specular light）。當一道光線射到表面時，它會被分成「折射」（refraction）和「反射」（reflection）兩個部分。反射部分是直接被反射且沒有進入表面的光；這就是我們所熟知的鏡面光照。折射部分是剩餘進入表面並被吸收的光；這就是我們所熟知的漫射光照。

這裡有一些細微之處，因為折射光並不會在接觸表面後立即被吸收。根據物理學，我們可以將光建模為一束能量，它會持續向前移動，直到失去所有能量；而光束失去能量的方式就是透過碰撞。每種材料都由微小的粒子組成，這些粒子可以與光線發生碰撞，如下圖所示。每次碰撞時，這些粒子會吸收部分或全部光線的能量，並將其轉化為熱能。

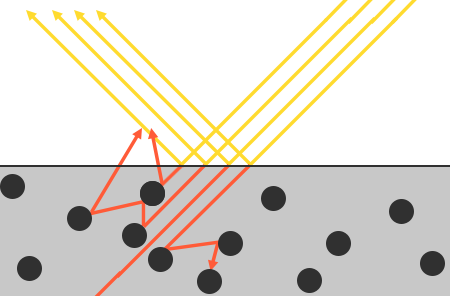
通常，並不是所有的能量都會被吸收，光線會繼續以（大多是）隨機的方向「散射」，然後與其他粒子碰撞，直到其能量耗盡或再次離開表面為止。重新從表面射出的光線，就會形成了我們觀察到的（漫射）顏色。

然而，在基於物理的渲染中，我們做了一個簡化的假設：所有折射光都會在一個非常小的撞擊區域內被吸收和散射，忽略了那些本來會在遠處離開表面的散射光線所產生的影響。專門考慮了這種效果的著色器技術被稱為「次表面散射」（subsurface scattering）技術，它們顯著提升了皮膚、大理石或蠟等材料的視覺品質，但代價是效能的犧牲。

當談到反射和折射時，還有一個額外的細微之處，那就是「金屬」（metallic）表面。與非金屬表面（也稱為「電介質」（dielectrics））相比，金屬表面對光的反應是不同的。金屬表面遵循相同的反射和折射原理，但所有折射光都會被直接吸收而不發生散射。這意味著金屬表面只會留下反射光或鏡面光；金屬表面不會顯示漫射顏色。由於金屬和電介質之間存在這種明顯的區別，它們在 PBR 管線中會被以不同的方式處理，我們將在本章後面進一步深入探討。

這種反射光和折射光之間的區別，讓我們引申出另一個關於能量守恆的觀察：它們是互斥的。無論有多少光能被反射，它都不會再被材料本身吸收。因此，在考慮了反射之後，剩餘進入表面作為折射光的能量，就是直接從反射中得到結果。

我們透過首先計算鏡面部分來維持這種能量守恆關係，鏡面部分代表了入射光能被反射的百分比。然後，折射光的部分會從鏡面部分直接計算得出：

float kS = calculateSpecularComponent(...); // reflection/specular fraction
float kD = 1.0 - kS;                        // refraction/diffuse  fraction

這樣一來，我們既能知道入射光反射了多少，又能知道折射了多少，同時也遵守了能量守恆原則。根據這種方法，折射/漫射和反射/鏡面光的總貢獻不可能超過 1.0，因此可以確保它們的能量總和永遠不會超過入射光的能量。這是我們在之前的光照章節中沒有考慮到的。

反射方程式（The reflectance equation）

這將我們帶到一個名為渲染方程式的東西，這是一個由一些非常聰明的人所提出來的精巧方程式，目前是我們用來類比光線視覺效果的最佳模型。基於物理的渲染嚴格遵循一個更專業化的渲染方程式版本，稱為「反射方程式」。為了正確理解 PBR，首先對反射方程式有一個扎實的理解是非常重要的：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

反射方程式一開始看起來令人望而生畏，但隨著我們對它進行拆解，你會發現它會慢慢變得有意義。要理解這個方程式，我們必須深入了解一點「輻射測量學」（radiometry）。輻射測量學是測量電磁輻射（包括可見光）的學科。我們可以利用幾種輻射測量量來測量表面和方向上的光線，但我們只會討論一個與反射方程式相關的量，也就是「輻射率」（radiance），在這裡用 \(L\) 表示。輻射率用於量化來自單一方向的光的大小或強度。由於輻射率是多個物理量的組合，一開始可能有點難以理解，所以我們先專注於這些物理量：

輻射通量（Radiant flux）：輻射通量 \(\Phi\) 是光源的傳輸能量，以瓦特（Watts）為單位。光是多個不同波長能量的集合總和，每個波長都與特定的（可見）顏色相關。因此，光源發出的能量可以被視為其所有不同波長的一個函數。波長介於 390 奈米（nm）到 700 奈米之間的範圍，被視為可見光光譜的一部分，也就是人眼能夠感知到的波長。下面這張圖片顯示了日光在不同波長下的能量：

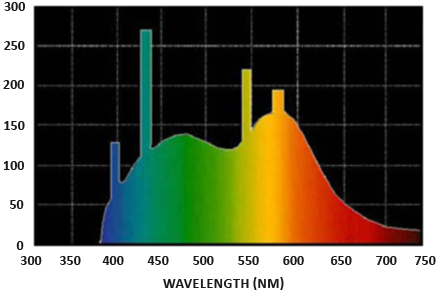
輻射通量測量的是這個由不同波長構成的函數的總面積。直接將這個波長測量值作為輸入有點不切實際，因此我們通常將輻射通量簡化為一個 RGB 編碼的光線顏色三元組（或者我們通常稱之為：光的顏色），而不是一個隨波長強度變化的函數。這種編碼確實會損失相當多的資訊，但對於視覺方面而言，這通常可以忽略不計。

立體角（Solid angle）：立體角，用 \(\omega\) 表示，告訴我們一個形狀投影到單位球體上的大小或面積。這個投影到單位球體上的形狀面積，就稱為「立體角」；你可以將立體角想像成一個有體積的方向：

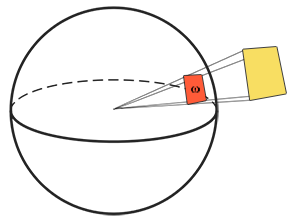
想像你是一個站在單位球體中心、朝著形狀方向看去的觀察者；你所看到的形狀輪廓大小就是立體角。

輻射強度（Radiant intensity）：輻射強度測量的是單位立體角下的輻射通量，或是光源在單位球體上投影區域的強度。舉例來說，對於一個向所有方向均勻發光的全向光源，輻射強度可以給我們它在特定區域（立體角）上的能量：

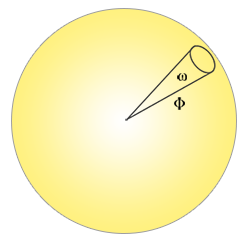
描述輻射強度的方程式定義如下：

\[I = \frac{d\Phi}{d\omega}\]

其中 \(I\) 是在立體角 \(\omega\) 上的輻射通量 \(\Phi\)。

有了輻射通量、輻射強度和立體角的知識後，我們終於可以描述輻射率的方程式了。輻射率被定義為在面積 \(A\) 上，輻射強度為 \(\Phi\) 的光線，在立體角 \(\omega\) 內觀測到的總能量：

\[L=\frac{d^2\Phi}{ dA d\omega \cos\theta}\]

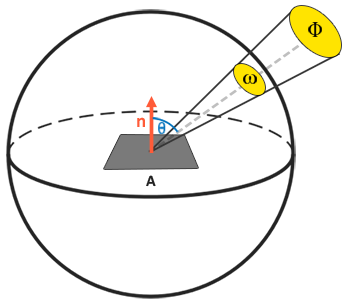
輻射率是衡量一個區域內光線總量的輻射測量量，它會根據光線與表面法線之間的入射（或稱作入射）角度 \(\theta\)，以 \(\cos \theta\) 進行縮放：光線越不直接照射到表面，它的強度就越弱；當它與表面垂直時，強度最強。這與我們在基礎光照章節中對漫射光照的感知類似，因為 \(\cos\theta\) 直接對應於光線方向向量和表面法線之間的點積：

float cosTheta = dot(lightDir, N);

輻射率方程式非常有用，因為它包含了我們感興趣的大部分物理量。如果我們將立體角 \(\omega\) 和面積 \(A\) 視為無限小，我們就可以使用輻射率來測量單一光線射到空間中單一點的通量。這種關係使我們能夠計算影響單一（片元）點的單一光線的輻射率；我們有效地將立體角 \(\omega\) 轉換為一個方向向量 \(\omega\)，將 \(A\) 轉換為一個點 \(p\)。透過這種方式，我們可以直接在著色器中使用輻射率，來計算單一光線在每個片元上的貢獻。

事實上，當涉及到輻射率時，我們通常關心的是照射到一個點 \(p\) 的所有入射光，這就是所有輻射率的總和，稱為「輻照度」（irradiance）。有了輻射率和輻照度的知識，我們就可以回到反射方程式：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

我們現在知道，渲染方程式中的 \(L\) 代表某個點 \(p\) 和某個入射的無限小立體角 \(\omega_i\) 的輻射率，這個立體角可以被視為一個入射方向向量 \(\omega_i\)。

請記住，\(\cos \theta\) 根據光線與表面的入射角來縮放能量，我們在反射方程式中可以看到它寫成 \(n \cdot \omega_i\)。反射方程式計算的是一個點 \(p\) 在方向 \(\omega_o\) 上的反射輻射率總和 \(L_o(p, \omega_o)\)，其中 \(\omega_o\) 是射向觀察者的出射方向。

換句話說：\(L_o\) 衡量的是從 \(\omega_o\) 方向看去，照射到點 \(p\) 的所有光線輻照度的反射總和。

反射方程式基於輻照度，也就是我們測量光線時所有入射輻射率的總和。這不僅僅是單一入射光方向，而是以點 \(p\) 為中心，在一個半球 \(\Omega\) 內的所有入射光方向的總和。半球可以被描述為一個以表面法線 \(n\) 為中心對齊的半個球體：

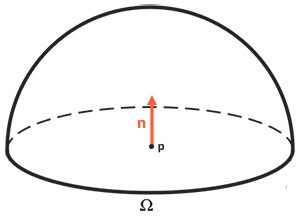
為了計算一個區域內（或者在半球的情況下，一個體積內）的數值總和，我們使用一種稱為「積分」的數學結構，它在反射方程式中被表示為在半球 \(\Omega\) 內對所有入射方向 \(d\omega_i\) 進行的 \(\int\) 運算。

積分測量的是一個函數的面積，可以透過解析或數值方法來計算。由於渲染和反射方程式都沒有解析解，我們需要透過數值方法來離散地求解這個積分。這意味著在半球 \(\Omega\) 內，對反射方程式的結果進行小而離散的步驟，然後將其結果除以步長來求平均值。這就是所謂的「黎曼和」（Riemann sum），我們可以大致將其視覺化為以下程式碼：

int steps = 100;
float sum = 0.0f;
vec3 P    = ...;
vec3 Wo   = ...;
vec3 N    = ...;
float dW  = 1.0f / steps;
for(int i = 0; i < steps; ++i)
{
    vec3 Wi = getNextIncomingLightDir(i);
    sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW;
}

透過將步長與 dW 相乘，總和將等於積分函數的總面積或體積。在反射方程式中，用於縮放每個離散步長的 dW 可以被視為 \(d\omega_i\)。從數學上講，\(d\omega_i\) 是我們計算積分的連續符號，雖然它與程式碼中的 dW 沒有直接關係（因為這是一個黎曼和的離散步長），但這樣思考有助於理解。請記住，採取離散步長總是會給我們一個函數總面積的近似值。細心的讀者會注意到，我們可以透過增加步長數量來提高黎曼和的精確度。

反射方程式將半球 \(\Omega\) 內所有入射光方向 \(\omega_i\) 的輻射率加總起來，並透過 \(f_r\) 進行縮放，這些光線照射到點 \(p\) 上，然後返回在觀察者方向上反射光的總和 \(L_o\)。入射輻射率可以來自我們所熟悉的光源，也可以來自測量每個入射方向輻射率的環境貼圖，我們將在 IBL 章節中討論這個部分。

現在，唯一剩下的未知數就是 \(f_r\) 符號，它被稱為 BRDF 或 雙向反射分佈函數（bidirectional reflective distribution function），它根據表面的材質屬性來縮放或加權入射輻射率。

BRDF

BRDF，或稱「雙向反射分佈函數」，是一個以入射（光線）方向 \(\omega_i\)、出射（視角）方向 \(\omega_o\)、表面法線 \(n\) 以及代表微表面粗糙度的表面參數 \(a\) 作為輸入的函數。BRDF 近似地描述了每個單獨的光線 \(\omega_i\) 在給定其材質屬性後，對不透明表面的最終反射光貢獻了多少。舉例來說，如果一個表面是完全光滑的（~就像鏡子一樣），那麼對於所有入射光線 \(\omega_i\) 來說，BRDF 函數都會返回 0.0，除了那條與出射光線 \(\omega_o\) 具有相同（反射）角度的光線，這時函數會返回 1.0。

BRDF 根據前面討論的微平面理論，近似地描述了材料的反射和折射屬性。一個 BRDF 要符合物理學原理，它必須遵守能量守恆定律，也就是反射光的總和絕不應超過入射光的總量。嚴格來說，Blinn-Phong 也被認為是一種 BRDF，它接收相同的 \(\omega_i\) 和 \(\omega_o\) 作為輸入。然而，Blinn-Phong 並不被視為基於物理的，因為它不遵循能量守恆原則。市面上有幾種基於物理的 BRDF 可用來近似表面對光的反應。然而，幾乎所有即時 PBR 渲染管線都使用一種稱為「Cook-Torrance BRDF」的 BRDF。

Cook-Torrance BRDF 同時包含漫射和鏡面部分：

\[f_r = k_d f_{lambert} + k_s f_{cook-torrance}\]

這裡的 \(k_d\) 是前面提到的入射光能量中被折射的比例，而 \(k_s\) 則是反射的比例。BRDF 的左側是方程式的漫射部分，在這裡用 \(f_{lambert}\) 表示。這就是所謂的「朗伯漫射」（Lambertian diffuse），類似於我們用於漫射著色的方法，它是一個常數因子，表示為：

\[ f_{lambert} = \frac{c}{\pi}\]

其中 \(c\) 是反照率（albedo）或表面顏色（可以想成是漫射表面紋理）。除以 \(\pi\) 是為了對漫射光進行歸一化，因為包含 BRDF 的積分（我們在IBL 章節中會提到）是以 \(\pi\) 進行縮放的。

你可能想知道這個朗伯漫射與我們之前使用的漫射光照有何關係：表面顏色乘以表面法線與光線方向之間的點積。點積仍然存在，但被移出了 BRDF，因為我們在 \(L_o\) 積分的結尾處找到了 \(n \cdot \omega_i\)。

BRDF 的漫射部分存在不同的方程式，它們看起來通常更真實，但計算成本也更高。然而，Epic Games 的結論是，朗伯漫射對於大多數即時渲染目的來說已經足夠了。

BRDF 的鏡面部分稍微進階一些，其描述如下：

\[ f_{CookTorrance} = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)} \]

Cook-Torrance 鏡面 BRDF 由三個函數和分母中的一個歸一化因子組成。每個符號 D、F 和 G 都代表一種函數，它們分別近似於表面反射屬性的特定部分。它們被定義為正態分佈函數（Distribution function）、菲涅耳方程式（Fresnel equation）和幾何函數（Geometry function）：

  • 正態分佈函數：近似了在表面粗糙度影響下，表面微平面與半向量的對齊程度；這是用來近似微平面的主要函數。
  • 幾何函數：描述了微平面的自遮蔽特性。當表面相對粗糙時，表面的微平面可能會遮蔽其他微平面，從而減少表面反射的光量。
  • 菲涅耳方程式：菲涅耳方程式描述了在不同表面角度下，表面反射的比例。

這些函數中的每一個都是它們物理對應物的近似，你會發現它們各自都有多個版本，旨在以不同的方式近似底層物理學；有些更真實，有些則更高效。挑選你想要使用的任何近似版本函數都是完全沒問題的。Epic Games 的 Brian Karis 在這裡對多種近似類型進行了大量的研究。我們將選擇 Epic Game 的 Unreal Engine 4 所使用的相同函數，也就是用於 D 的 Trowbridge-Reitz GGX，用於 F 的 Fresnel-Schlick 近似，以及用於 G 的 Smith’s Schlick-GGX。

正態分佈函數（Normal distribution function）

正態分佈函數 \(D\) 統計性地近似了與（半）向量 \(h\) 精確對齊的微平面的相對表面積。有大量的 NDF 可以根據某些粗糙度參數，統計性地近似微平面的整體對齊情況，我們將要使用的是被稱為 Trowbridge-Reitz GGX 的函數：

\[ NDF_{GGX TR}(n, h, \alpha) = \frac{\alpha^2}{\pi((n \cdot h)^2 (\alpha^2 - 1) + 1)^2} \]

在這裡，\(h\) 是用來與表面微平面進行測量的半向量，而 \(a\) 則是表面粗糙度的量度。如果我們在不同的粗糙度參數下，將 \(h\) 作為表面法線和光線方向之間的半向量，我們將得到以下的視覺結果：

當粗糙度較低（因此表面光滑）時，在一個小半徑範圍內，有高度集中的微平面與半向量對齊。由於這種高度集中，NDF 顯示出一個非常明亮的光斑。然而，在粗糙的表面上，微平面以更隨機的方向對齊，你會發現有更多數量的半向量 \(h\) 與微平面有些對齊（但集中度較低），這給我們帶來了更偏灰色的結果。

在 GLSL 中，Trowbridge-Reitz GGX 正態分佈函數轉譯為以下程式碼：

float DistributionGGX(vec3 N, vec3 H, float a)
{
    float a2     = a*a;
    float NdotH  = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;

    float nom    = a2;
    float denom  = (NdotH2 * (a2 - 1.0) + 1.0);
    denom        = PI * denom * denom;

    return nom / denom;
}

幾何函數（Geometry function）

幾何函數統計性地近似了微表面細節彼此遮蔽，導致光線被遮擋的相對表面積。

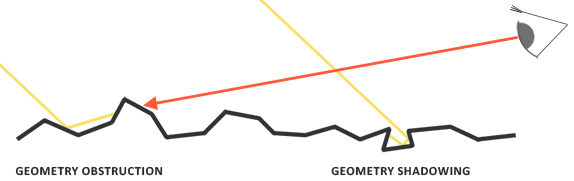
與 NDF 類似，幾何函數也將材質的粗糙度參數作為輸入，粗糙的表面有更高的機率遮蔽微平面。我們將使用的幾何函數是 GGX 和 Schlick-Beckmann 近似法的組合，稱為 Schlick-GGX：

\[ G_{SchlickGGX}(n, v, k) = \frac{n \cdot v} {(n \cdot v)(1 - k) + k } \]

這裡的 \(k\) 是根據我們是將幾何函數用於直接光照還是 IBL 光照，對 \(\alpha\) 進行的重新映射：

\[ k_{direct} = \frac{(\alpha + 1)^2}{8} \] \[ k_{IBL} = \frac{\alpha^2}{2} \]

請注意，\(\alpha\) 的值可能會因你的引擎如何將粗糙度轉換為 \(\alpha\) 而有所不同。在接下來的章節中，我們將詳細討論這種重新映射如何以及在哪裡變得相關。

為了有效地近似幾何特性，我們需要同時考慮視角方向（幾何遮擋）和光線方向向量（幾何陰影）。我們可以使用「Smith 方法」將這兩者都納入考量：

\[ G(n, v, l, k) = G_{sub}(n, v, k) G_{sub}(n, l, k) \]

利用帶有 Schlick-GGX 作為 \(G_{sub}\) 的 Smith 方法，在不同的粗糙度 R 下，會產生以下的視覺外觀：

幾何函數是一個介於 [0.0, 1.0] 之間的乘數，其中 1.0（或白色）表示沒有微平面陰影，0.0（或黑色）則表示完全的微平面陰影。

在 GLSL 中，幾何函數轉譯為以下程式碼：

float GeometrySchlickGGX(float NdotV, float k)
{
    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}

float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx1 = GeometrySchlickGGX(NdotV, k);
    float ggx2 = GeometrySchlickGGX(NdotL, k);

    return ggx1 * ggx2;
}

菲涅耳方程式（Fresnel equation）

菲涅耳方程式（發音為 Freh-nel）描述了反射光與折射光的比例，這個比例會隨著我們觀察表面的角度而變化。當光線射到表面時，菲涅耳方程式會根據表面到視角的角度，告訴我們光線被反射的百分比。從這個反射比例和能量守恆原理，我們可以直接得到光線的折射部分。

當我們正對著一個表面看時，每個表面或材料都有一定程度的「基礎反射率」（base reflectivity），但當我們從一個角度觀察表面時，所有的反射都會比表面的基礎反射率更明顯。你可以自己檢驗這一點，看看你（假設是）木製/金屬製的書桌，從垂直視角看時，它有一定的基礎反射率，但當你從一個接近 90 度的角度看書桌時，你會發現反射變得更加明顯。從理論上講，當從完美的 90 度角觀察時，所有表面都會完全反射光線。這種現象被稱為「菲涅耳」（Fresnel），並由菲涅耳方程式來描述。

菲涅耳方程式是一個相當複雜的方程式，但幸運的是，我們可以利用「Fresnel-Schlick 近似法」來近似菲涅耳方程式：

\[ F_{Schlick}(h, v, F_0) = F_0 + (1 - F_0) ( 1 - (h \cdot v))^5 \]

\(F_0\) 代表表面的基礎反射率，我們使用一種稱為 折射率指數（indices of refraction）或 IOR 的東西來計算它。正如你在球體表面上看到的，我們越是朝著掠射角（grazing angles）看（半向量-視角達到 90 度），菲涅耳效應就越強，反射也越強：

菲涅耳方程式有一些微妙之處。其中之一是，Fresnel-Schlick 近似法實際上只為「電介質」或非金屬表面定義。對於「導體」（conductor）表面（金屬），使用折射率指數來計算基礎反射率並不完全適用，我們需要為導體使用一個完全不同的菲涅耳方程式。

由於這很不方便，我們透過預先計算表面在「正入射」（normal incidence）（\(F_0\)）下，也就是當視角為 0 度時，正對著表面看時的反應，來進一步近似。然後我們根據視角，按照 Fresnel-Schlick 近似法對這個值進行插值，這樣我們就可以對金屬和非金屬使用同一個方程式了。

表面在正入射下的反應，或稱基礎反射率，可以在大型資料庫中找到，比如這裡，下面列出了一些 Naty Hoffman 課程筆記中較常見的值：

Material\(F_0\) (Linear)\(F_0\) (sRGB)Color
Water(0.02, 0.02, 0.02) (0.15, 0.15, 0.15)  
Plastic / Glass (Low)(0.03, 0.03, 0.03)(0.21, 0.21, 0.21)
Plastic High(0.05, 0.05, 0.05)(0.24, 0.24, 0.24)
Glass (high) / Ruby(0.08, 0.08, 0.08)(0.31, 0.31, 0.31)
Diamond(0.17, 0.17, 0.17)(0.45, 0.45, 0.45)
Iron(0.56, 0.57, 0.58)(0.77, 0.78, 0.78)
Copper(0.95, 0.64, 0.54)(0.98, 0.82, 0.76)
Gold(1.00, 0.71, 0.29)(1.00, 0.86, 0.57)
Aluminium(0.91, 0.92, 0.92)(0.96, 0.96, 0.97)
Silver(0.95, 0.93, 0.88)(0.98, 0.97, 0.95)

這裡有趣的一點是，對於所有電介質表面來說，基礎反射率從未超過 0.17（這是一個例外而非規則），而對於導體來說，基礎反射率要高得多，並且（大多）介於 0.5 到 1.0 之間。此外，對於導體（或金屬表面），基礎反射率是帶有顏色的。這就是為什麼 \(F_0\) 會以 RGB 三元組的形式呈現（正入射下的反射率會因波長而異）；這是我們只在金屬表面上才看得到的現象。

與電介質表面相比，金屬表面的這些獨特屬性催生了一種稱為「金屬度工作流程」（metallic workflow）的方法。在金屬度工作流程中，我們透過一個稱為 金屬度（metalness）的額外參數來創作表面材質，這個參數描述了一個表面是金屬還是非金屬。

理論上，一個材質的金屬度是二元的：它不是金屬就是非金屬，不可能兩者都是。然而，大多數渲染管線允許以 0.0 到 1.0 之間線性地配置表面的金屬度。這主要是因為材質紋理精度的限制。舉例來說，一個金屬表面上覆蓋著細小的（非金屬）灰塵/沙粒/刮痕，就很難用二元的金屬度值來渲染。

透過預先計算電介質和導體的 \(F_0\)，我們可以對這兩種表面使用相同的 Fresnel-Schlick 近似法，但如果我們有一個金屬表面，我們必須為基礎反射率上色。我們通常透過以下方式來實現：

vec3 F0 = vec3(0.04);
F0      = mix(F0, surfaceColor.rgb, metalness);

我們定義了一個近似於大多數電介質表面的基礎反射率。這又是一個近似值，因為 \(F_0\) 是取大多數常見電介質的平均值。0.04 的基礎反射率適用於大多數電介質，並且在無需額外創作表面參數的情況下，也能產生符合物理學原理的結果。然後，根據表面的金屬度，我們要麼使用電介質的基礎反射率，要麼使用以表面顏色創作的 \(F_0\)。因為金屬表面會吸收所有折射光，它們沒有漫射反射，所以我們可以將表面顏色紋理直接用作它們的基礎反射率。

在程式碼中，Fresnel Schlick 近似法轉譯為：

vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
    return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}

其中 cosTheta 是表面法線 \(n\) 和半向量 \(h\)（或視角 \(v\)）方向之間的點積結果。

Cook-Torrance 反射方程式（Cook-Torrance reflectance equation）

在描述了 Cook-Torrance BRDF 的每個組成部分之後，我們現在可以將這個基於物理的 BRDF 包含到最終的反射方程式中：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

然而，這個方程式在數學上並非完全正確。你可能會記得，菲涅耳項 \(F\) 代表了在表面上被反射的光線比例。這實際上就是我們的比例 \(k_s\)，這意味著反射方程式的鏡面（BRDF）部分隱含地包含了反射比例 \(k_s\)。鑑於此，我們最終的反射方程式變為：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

這個方程式現在完整描述了一個基於物理的渲染模型，這個模型通常被認為是我們普遍理解的 PBR。如果你還沒有完全理解如何將所有討論過的數學內容放入程式碼中也別擔心。在接下來的章節裡，我們將探索如何利用反射方程式，讓我們的渲染光照產生更符合物理原理的結果，到那時，所有零散的部分應該會慢慢地組合起來。

創作 PBR 材質

在了解 PBR 的底層數學模型後，我們將透過描述藝術家們通常如何創作表面的物理屬性來結束這次討論，這些屬性我們可以將其直接輸入到 PBR 方程式中。PBR 管線所需的每一個表面參數都可以透過紋理來定義或建模。使用紋理讓我們能夠以每個片元為基礎，精準控制每個特定的表面點應該如何對光線作出反應：無論該點是金屬的、粗糙的還是光滑的，以及表面如何回應不同波長的光線。

下面你將看到一個 PBR 管線中經常會出現的紋理列表，以及當它們被應用於 PBR 渲染器時所產生的視覺輸出：

反照率（Albedo）：反照率紋理為每個紋素指定表面的顏色，如果該紋素是金屬，則指定其基礎反射率。這在很大程度上與我們之前使用的漫射紋理類似，但所有光照資訊都從紋理中被提取出來。漫射紋理通常在圖像中帶有輕微的陰影或變暗的裂縫，這是在反照率紋理中不想要的；它應該只包含表面的顏色（或折射吸收係數）。

法線（Normal）：法線貼圖紋理與我們在法線貼圖章節中使用的完全一樣。法線貼圖讓我們能夠為每個片元指定一個獨特的法線，從而產生表面比其實際平坦對應物更「凹凸不平」的錯覺。

金屬度（Metallic）：金屬度貼圖為每個紋素指定其是否為金屬。根據 PBR 引擎的設定方式，藝術家可以將金屬度創作為灰階值或二進位的黑色或白色。

粗糙度（Roughness）：粗糙度貼圖以每個紋素為基礎指定表面的粗糙程度。採樣到的粗糙度值會影響表面微平面的統計取向。較粗糙的表面會產生更寬、更模糊的反射，而光滑的表面則會產生集中且清晰的反射。有些 PBR 引擎會期望一個 光滑度（smoothness）貼圖而不是粗糙度貼圖，一些藝術家認為這更直觀。這些值在被採樣時會被轉換（1.0 - smoothness）為粗糙度。

AO：環境光遮蔽（ambient occlusion）或 AO 貼圖指定了表面以及潛在周圍幾何體的額外陰影因子。舉例來說，如果我們有一個磚塊表面，反照率紋理不應該在磚塊的裂縫中有陰影資訊。然而，AO 貼圖會指定這些變暗的邊緣，因為光線更難從這些地方逃逸。在光照階段的最後考慮環境光遮蔽，可以顯著提升場景的視覺品質。網格/表面的環境光遮蔽貼圖是手動生成，或在 3D 建模程式中預先計算的。

藝術家們以每個紋素為基礎來設定和調整這些基於物理的輸入值，並且可以根據現實世界材料的物理表面屬性來創作他們的紋理值。這是 PBR 渲染管線的最大優勢之一，因為表面的這些物理屬性保持不變，無論環境或光照設定如何，這使得藝術家更容易獲得符合物理原理的結果。在 PBR 管線中創作的表面可以輕鬆地在不同的 PBR 渲染引擎之間共享，無論它們處於何種環境中，外觀都會是正確的，因此看起來也更自然。

延伸閱讀