PBR • 漫射輻照度 (Diffuse-irradiance)

第四十二章

PBR • 漫射輻照度 (Diffuse-irradiance)

發布時間：2025-08-04 閱讀時間：51 分鐘

IBL，全名為 image based lighting，是一種透過將周圍環境視為一個大型光源，而非像前一章節那樣使用直接的解析光源來點亮物體的技術。這通常是透過對環境貼圖（cubemap environment map）進行操作來實現的，這些環境貼圖可以來自真實世界，或是從 3D 場景中生成。透過這些處理，我們可以直接在光照方程式中使用它，將每個 cubemap 紋素（texel）視為一個光源發射器。這樣一來，我們就能有效地捕捉環境的整體光照和氛圍，讓物體更有「身處」於其環境中的感覺。

由於基於圖片的光照演算法（IBL）捕捉了某些（全域）環境的光照，其輸入被認為是一種更精確的環境光形式，甚至是全域照明的一種粗略近似。這使得 IBL 對於 PBR 來說非常有趣，因為當我們將環境的光照考慮進去時，物體看起來會更加符合物理真實性。

為了開始將 IBL 引入我們的 PBR 系統，讓我們先快速回顧一下反射方程式（reflectance equation）：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

就像前面描述過的，我們的主要目標是解出對半球 \(\Omega\) 上所有入射光方向 \(w_i\) 的積分。在前面章節中，解這個積分很簡單，因為我們事先知道只有那幾個特定方向 \(w_i\) 的光會對積分有所貢獻。然而這一次，來自周圍環境的每一個入射光方向 \(w_i\) 都可能帶有一些輻射（radiance），這使得解這個積分變得不再那麼簡單。這給了解決這個積分帶來了兩個主要的要求：

我們需要某種方法，能根據任何一個方向向量 \(w_i\) 來獲取場景的輻射。
求解這個積分必須快速且即時。

現在，第一個要求相對簡單。我們已經暗示過了，但表示環境或場景輻照度（irradiance）的一種方法，就是以（經過處理的）環境立方體貼圖（cubemap）的形式。給定這樣一個立方體貼圖，我們可以將立方體貼圖的每個紋素（texel）視為一個單獨的光源發射器。透過使用任何方向向量 \(w_i\) 來採樣這個立方體貼圖，我們就能夠從該方向獲取場景的輻射。

因此，根據任何方向向量 \(w_i\) 來獲取場景輻射，就變得非常簡單了：

vec3 radiance = texture(_cubemapEnvironment, w_i).rgb;

然而，解這個積分需要我們不僅從一個方向，而是從半球 \(\Omega\) 上的所有可能方向 \(w*i\) 來採樣環境貼圖，這對於每一個片元著色器（fragment shader）的呼叫來說，開銷實在太大了。為了以更有效率的方式解出這個積分，我們需要對大部分的計算進行「預處理」（pre-process）或稱為「預運算」（pre-compute）。為此，我們必須更深入地研究反射方程式：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

仔細觀察這個反射方程式，我們發現 BRDF 的漫射（diffuse）項 \(k_d\) 和鏡面反射（specular）項 \(k_s\) 彼此是獨立的，所以我們可以將積分拆成兩部分：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i + \int\limits_{\Omega} (k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

透過將積分拆成兩部分，我們可以分別專注於漫射項和鏡面反射項；而本章節的重點將放在漫射積分上。

我們再仔細看看漫射積分，會發現漫射蘭伯特（lambert）項是一個常數項（顏色 \(c\)、折射率 \(k_d\) 以及 \(\pi\) 在積分中都是常數），並且不依賴於任何積分變數。基於這一點，我們可以將常數項移出漫射積分：

\[ L_o(p,\omega_o) = k_d\frac{c}{\pi} \int\limits_{\Omega} L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

這讓我們的積分只取決於 \(w*i\)（假設 \(p\) 位於環境貼圖的中心）。有了這個認知，我們可以透過「卷積」（convolution）來計算或「預運算」（pre-compute）一個新的立方體貼圖，這個貼圖在每個採樣方向（或紋素） \(w_o\) 中，儲存了漫射積分的結果。

卷積是對資料集中的每個項目應用某種運算，同時考慮到資料集中的所有其他項目；這裡的資料集就是場景的輻射或環境貼圖。因此，對於立方體貼圖中的每個採樣方向，我們都會將半球 \(\Omega\) 上的所有其他採樣方向納入考慮。

為了對環境貼圖進行卷積，我們針對每個輸出 \(w_o\) 採樣方向，透過在半球 \(\Omega\) 上離散地採樣大量方向 \(w_i\) 並取其輻射的平均值來解這個積分。我們用來建構採樣方向 \(w_i\) 的半球，是朝向我們正在進行卷積的輸出 \(w_o\) 採樣方向。

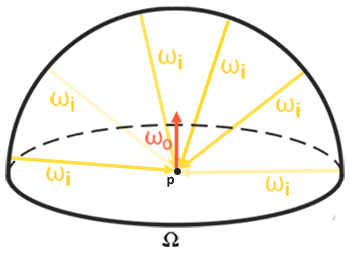
這個預運算的立方體貼圖，在每個採樣方向 \(w_o\) 中儲存了積分結果，可以被視為擊中某個沿著方向 \(w_o\) 對齊的表面，場景中所有間接漫射光的預運算總和。由於這個經過卷積的立方體貼圖能讓我們從任何方向 \(w_o\) 直接採樣場景的（預運算）輻照度（irradiance），因此它被稱為輻照度圖（irradiance map）。

輻射方程式也依賴於一個位置 \(p\)，我們假設它位於輻照度圖的中心。這確實意味著所有間接漫射光都必須來自單一的環境貼圖，這可能會破壞真實感（尤其是在室內場景）。渲染引擎透過在場景中放置「反射探測器」（reflection probes）來解決這個問題，每個反射探測器都會計算其周圍環境的專屬輻照度圖。如此一來，位置 \(p\) 的輻照度（和輻射）就是其最接近的反射探測器之間插值後的輻照度。目前，我們先假設我們總是從環境貼圖的中心進行採樣。

下面是一個立方體環境貼圖及其生成的輻照度圖範例（圖片由 wave engine 提供），它對每個方向 \(w_o\) 的場景輻射進行了平均。

透過將卷積結果儲存在每個立方體貼圖紋素中（朝向 \(w_o\) 方向），輻照度圖會呈現出環境的平均顏色或光照顯示。從這個環境貼圖中採樣任何方向，都能給我們該特定方向的場景輻照度。

PBR 與 HDR

在上一章節中，我們簡單提過：在 PBR 管線中，將場景光照的高動態範圍（high dynamic range, HDR）納入考量是極其重要的。由於 PBR 的大多數輸入都基於真實的物理屬性和測量，因此將入射光值與其物理等效值緊密匹配是合情合理的。無論我們是憑經驗來猜測每個光源的輻射通量（radiant flux），還是使用其直接的物理等效值，一個簡單的燈泡和太陽之間的差異都是巨大的。如果不使用 HDR 渲染環境，就無法正確指定每個光源的相對強度。

因此，PBR 和 HDR 密不可分，但這一切與基於圖片的光照有什麼關聯呢？我們在上一章節看到，讓 PBR 在 HDR 環境中運作相對容易。然而，由於在基於圖片的光照中，我們是將環境的間接光強度建立在環境立方體貼圖的顏色值上，因此我們需要某種方法將光照的高動態範圍儲存到環境貼圖中。

我們迄今為止用作立方體貼圖（例如用作天空盒）的環境貼圖，都是低動態範圍（LDR）的。我們直接使用來自單獨面圖片的顏色值，其範圍介於 0.0 和 1.0 之間，並按原樣處理它們。雖然這對於視覺輸出可能沒問題，但當將它們作為物理輸入參數時，就行不通了。

輻射度 HDR 檔案格式

此時，就輪到輻射度檔案格式（radiance file format）登場了。輻射度檔案格式（副檔名為 .hdr）將一個完整的立方體貼圖及其所有 6 個面都儲存為浮點數資料。這讓我們可以指定超出 0.0 到 1.0 範圍的顏色值，以賦予光源正確的顏色強度。該檔案格式還使用了一個巧妙的技巧來儲存每個浮點數值：它不是每個通道使用 32 位元，而是每個通道使用 8 位元，並將顏色的 Alpha 通道用作指數（這會帶來精度的損失）。這種方法效果很好，但需要解析程式將每個顏色重新轉換為其浮點數等效值。

網路上有相當多免費的輻射度 HDR 環境貼圖，例如 sIBL archive，你可以在下面看到一個範例：

這可能和你預期的不太一樣，因為這張圖片看起來扭曲了，也沒有顯示我們之前看到的環境貼圖那樣獨立的 6 個立方體面。這張環境貼圖是從一個球體投影到一個平面上的，這樣我們就能更方便地將環境儲存到一個單一的圖片中，這種圖片被稱為等距柱狀投影圖（equirectangular map）。這樣做有一個小小的缺點，就是大部分的視覺解析度都儲存在水平視圖方向，而底部和頂部方向的解析度則較低。但在大多數情況下，這是一個不錯的折衷方案，因為在幾乎所有渲染器中，你都會發現在水平視角方向上有最多有趣的光照和周圍環境。

HDR 和 stb_image.h

直接載入輻射度 HDR 圖片需要對檔案格式有一些了解，雖然不是非常困難，但仍然很麻煩。幸運的是，廣受歡迎的單標頭檔函式庫 stb_image.h 支援直接將輻射度 HDR 圖片載入為一個浮點數陣列，這完美地符合我們的需求。將 stb_image 加入你的專案後，載入 HDR 圖片現在變得如此簡單：

#include "stb_image.h"
[...]

stbi_set_flip_vertically_on_load(true);
int width, height, nrComponents;
float *data = stbi_loadf("newport_loft.hdr", &width, &height, &nrComponents, 0);
unsigned int hdrTexture;
if (data)
{
    glGenTextures(1, &hdrTexture);
    glBindTexture(GL_TEXTURE_2D, hdrTexture);
    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, width, height, 0, GL_RGB, GL_FLOAT, data);

    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

    stbi_image_free(data);
}
else
{
    std::cout << "Failed to load HDR image." << std::endl;
}

stb_image.h 會自動將 HDR 值映射為一個浮點數值列表：預設每個通道 32 位元，每個顏色 3 個通道。這就是我們將等距柱狀 HDR 環境貼圖儲存到一個 2D 浮點數紋理所需的一切。

從等距柱狀投影圖到立方體貼圖

我們可以直接使用等距柱狀投影圖來進行環境查詢，但這些操作的開銷可能相對較大，而直接的立方體貼圖採樣則效能更佳。因此，在本章節中，我們將首先把等距柱狀圖片轉換成立方體貼圖，以進行進一步的處理。請注意，在這個過程中，我們也會展示如何採樣等距柱狀圖，使其就像一個 3D 環境貼圖一樣，你可以自由選擇你喜歡的解決方案。

要將等距柱狀圖片轉換成立方體貼圖，我們需要渲染一個（單位）立方體，並從內部將等距柱狀圖投影到立方體的所有面上，然後將立方體每一側的 6 張圖片作為立方體貼圖的面。這個立方體的頂點著色器只是簡單地將立方體原樣渲染出來，並將其局部位置作為 3D 採樣向量傳遞給片元著色器：

#version 330 core
layout (location = 0) in vec3 aPos;

out vec3 localPos;

uniform mat4 projection;
uniform mat4 view;

void main()
{
    localPos = aPos;
    gl_Position =  projection * view * vec4(localPos, 1.0);
}

對於片元著色器，我們對立方體的每個部分進行著色，就像我們將等距柱狀圖整齊地摺疊到立方體的每一側一樣。為了實現這一點，我們將從立方體局部位置插值而來的片元採樣方向，然後使用這個方向向量和一些三角學魔法（從球座標到笛卡爾座標）來採樣等距柱狀圖，使其本身就像一個立方體貼圖。我們直接將結果儲存到立方體面的片元上，這應該就是我們需要做的全部了：

#version 330 core
out vec4 FragColor;
in vec3 localPos;

uniform sampler2D equirectangularMap;

const vec2 invAtan = vec2(0.1591, 0.3183);
vec2 SampleSphericalMap(vec3 v)
{
    vec2 uv = vec2(atan(v.z, v.x), asin(v.y));
    uv *= invAtan;
    uv += 0.5;
    return uv;
}

void main()
{
    vec2 uv = SampleSphericalMap(normalize(localPos)); // make sure to normalize localPos
    vec3 color = texture(equirectangularMap, uv).rgb;

    FragColor = vec4(color, 1.0);
}

如果你在場景中心渲染一個給定 HDR 等距柱狀圖的立方體，你會得到類似下圖的畫面：

這證明我們確實有效地將等距柱狀圖片映射到了立方體形狀上，但這還沒幫我們把來源的 HDR 圖片轉換成立方體貼圖紋理。為了達成這個目標，我們必須渲染同一個立方體 6 次，每次都朝著立方體的一個面看，同時用幀緩衝區物件來記錄其視覺結果：

unsigned int captureFBO, captureRBO;
glGenFramebuffers(1, &captureFBO);
glGenRenderbuffers(1, &captureRBO);

glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, captureRBO);

當然，我們也會生成相對應的立方體貼圖顏色紋理，並為它的 6 個面預先分配記憶體：

unsigned int envCubemap;
glGenTextures(1, &envCubemap);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
for (unsigned int i = 0; i < 6; ++i)
{
    // note that we store each face with 16 bit floating point values
    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F,
                 512, 512, 0, GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

接下來剩下的工作就是將等距柱狀 2D 紋理捕捉到立方體貼圖的面上。

我不會詳細說明這些細節，因為程式碼的細節在幀緩衝區和點光源陰影章節中已經討論過了，但它基本上就是設定 6 個不同的視圖矩陣（每個都朝向立方體的一個面），設定一個 fov 為 90 度的投影矩陣來捕捉整個面，然後渲染一個立方體 6 次，將結果儲存在浮點數幀緩衝區中：

glm::mat4 captureProjection = glm::perspective(glm::radians(90.0f), 1.0f, 0.1f, 10.0f);
glm::mat4 captureViews[] =
{
   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 1.0f,  0.0f,  0.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(-1.0f,  0.0f,  0.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  1.0f,  0.0f), glm::vec3(0.0f,  0.0f,  1.0f)),
   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, -1.0f,  0.0f), glm::vec3(0.0f,  0.0f, -1.0f)),
   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  0.0f,  1.0f), glm::vec3(0.0f, -1.0f,  0.0f)),
   glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  0.0f, -1.0f), glm::vec3(0.0f, -1.0f,  0.0f))
};

// convert HDR equirectangular environment map to cubemap equivalent
equirectangularToCubemapShader.use();
equirectangularToCubemapShader.setInt("equirectangularMap", 0);
equirectangularToCubemapShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, hdrTexture);

glViewport(0, 0, 512, 512); // don't forget to configure the viewport to the capture dimensions.
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
for (unsigned int i = 0; i < 6; ++i)
{
    equirectangularToCubemapShader.setMat4("view", captureViews[i]);
    glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0,
                           GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, envCubemap, 0);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    renderCube(); // renders a 1x1 cube
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);

我們取用幀緩衝區的顏色附件，並為立方體貼圖的每個面切換其紋理目標，將場景直接渲染到立方體貼圖的其中一個面上。一旦這個流程完成（我們只需執行一次），立方體貼圖 envCubemap 就會是我們原始 HDR 圖片的立方體貼圖環境版本。

接下來，讓我們撰寫一個非常簡單的天空盒著色器來測試這個立方體貼圖，將它顯示在我們周圍：

#version 330 core
layout (location = 0) in vec3 aPos;

uniform mat4 projection;
uniform mat4 view;

out vec3 localPos;

void main()
{
    localPos = aPos;

    mat4 rotView = mat4(mat3(view)); // remove translation from the view matrix
    vec4 clipPos = projection * rotView * vec4(localPos, 1.0);

    gl_Position = clipPos.xyww;
}

請注意這裡的 xyww 技巧，它確保渲染的立方體片元的深度值總是 1.0，也就是最大深度值，這在立方體貼圖章節中已經描述過了。也請注意，我們需要將深度比較函式改為 GL_LEQUAL：

glDepthFunc(GL_LEQUAL);

然後，片元著色器會直接使用立方體的局部片元位置來採樣立方體貼圖環境圖：

#version 330 core
out vec4 FragColor;

in vec3 localPos;

uniform samplerCube environmentMap;

void main()
{
    vec3 envColor = texture(environmentMap, localPos).rgb;

    envColor = envColor / (envColor + vec3(1.0));
    envColor = pow(envColor, vec3(1.0/2.2));

    FragColor = vec4(envColor, 1.0);
}

我們使用插值的立方體頂點位置來採樣環境貼圖，這些位置直接對應到正確的採樣方向向量。由於我們忽略了攝影機的平移分量，在立方體上渲染這個著色器應該會給你一個不移動的背景環境貼圖。此外，由於我們將環境貼圖的 HDR 值直接輸出到預設的 LDR 幀緩衝區，我們需要對顏色值進行適當的色調映射（tone map）。還有，幾乎所有 HDR 貼圖預設都處於線性色彩空間中，因此我們在寫入預設幀緩衝區之前需要套用伽瑪校正。

現在，在之前渲染的球體上渲染採樣的環境貼圖，看起來應該像這樣：

呼… 雖然花了不少工夫，但我們總算成功地讀取了 HDR 環境貼圖，將其從等距柱狀投影轉換成立方體貼圖，並將這個 HDR 立方體貼圖作為天空盒渲染到場景中。此外，我們還建立了一個小型系統，可以在立方體貼圖的所有 6 個面上進行渲染，這在對環境貼圖進行「卷積」（convoluting）時會再次派上用場。你可以在這裡找到整個轉換過程的原始碼。

立方體貼圖卷積

就像本章節一開始描述的那樣，我們的主要目標是，給定一個立方體環境貼圖形式的場景輻照度，來解出所有間接漫射光的積分。我們知道，透過沿著方向 \(w_i\) 採樣 HDR 環境貼圖，我們可以得到該特定方向的場景輻射 \(L(p, w_i)\)。為了求解這個積分，我們必須為每個片元從半球 \(\Omega\) 內所有可能的方向採樣場景的輻射。

然而，在計算上，不可能即時地從 \(\Omega\) 內的每個可能方向採樣環境光，因為可能的方向數量在理論上是無限的。不過，我們可以透過取有限數量的方向或樣本，這些樣本均勻分佈或隨機地從半球內部採樣，來近似方向數量，從而得到一個相當準確的輻照度近似值；這實際上就是離散地求解積分 \(\int\)。

然而，在即時渲染中，對每個片元都這樣做仍然過於昂貴，因為需要大量的樣本才能得到不錯的結果，所以我們需要進行「預運算」（pre-compute）。既然半球的方向決定了我們從哪裡捕捉輻照度，我們就可以預先計算圍繞所有出射方向 \(w_o\) 的所有可能半球方向的輻照度：

\[ L_o(p,\omega_o) = k_d\frac{c}{\pi} \int\limits_{\Omega} L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

在光照階段中，給定任何方向向量 \(w_i\)，我們就可以採樣這個預運算的輻照度圖，以取得來自方向 \(w_i\) 的總漫射輻照度。為了確定一個片元表面上的間接漫射（輻射）光量，我們只需取得圍繞其表面法線所對齊的半球的總輻照度。因此，獲取場景的輻照度就變得非常簡單了：

vec3 irradiance = texture(irradianceMap, N).rgb;

現在，要生成輻照度圖，我們需要對轉換成立方體貼圖的環境光照進行卷積。假設對於每個片元，其表面的半球都沿著法向量 \(N\) 定向，那麼對立方體貼圖進行卷積就等於計算在沿著 \(N\) 定向的半球 \(\Omega\) 內，每個方向 \(w_i\) 的總平均輻射。

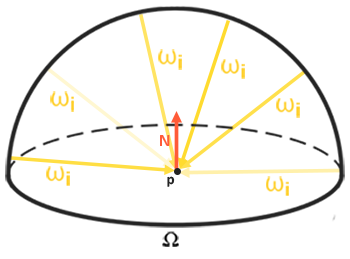
幸運的是，本章節所有繁瑣的設定並非徒勞無功，因為我們現在可以直接拿這個轉換後的立方體貼圖，在片元著色器中對它進行卷積，並使用一個能渲染到所有 6 個面方向的幀緩衝區，將結果捕捉到一個新的立方體貼圖中。由於我們已經為將等距柱狀環境貼圖轉換成立方體貼圖而設定過這個流程，所以我們可以採用完全相同的方法，只是使用不同的片元著色器：

#version 330 core
out vec4 FragColor;
in vec3 localPos;

uniform samplerCube environmentMap;

const float PI = 3.14159265359;

void main()
{
    // the sample direction equals the hemisphere's orientation
    vec3 normal = normalize(localPos);

    vec3 irradiance = vec3(0.0);

    [...] // convolution code

    FragColor = vec4(irradiance, 1.0);
}

其中 environmentMap 是我們從等距柱狀 HDR 環境貼圖轉換而來的 HDR 立方體貼圖。

對環境貼圖進行卷積有很多種方法，但對於本章節，我們將針對每個立方體貼圖紋素，沿著圍繞採樣方向定向的半球 \(\Omega\)，生成固定數量的採樣向量，並將結果取平均。這些固定數量的採樣向量將均勻分佈在半球內部。請注意，積分是一個連續函式，而給定固定數量的採樣向量對其函式進行離散採樣將會是一個近似值。我們使用的採樣向量越多，對積分的近似就越好。

反射方程式的積分 \(\int\) 圍繞著立體角 \(dw\) 進行，這處理起來相當困難。我們將不對立體角 \(dw\) 進行積分，而是對其等效的球座標 \(\theta\) 和 \(\phi\) 進行積分。

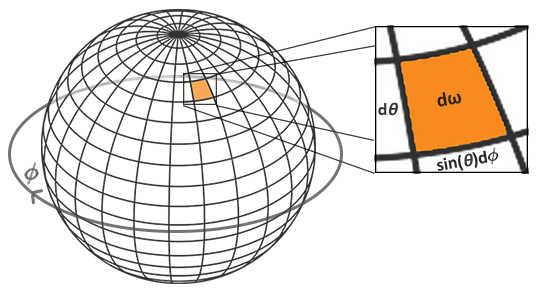
我們使用極方位角（polar azimuth）\(\phi\) 來在半球的環上進行採樣，範圍介於 \(0\) 和 \(2\pi\) 之間；並使用傾角天頂角（inclination zenith）\(\theta\) 來採樣半球不斷增大的環，範圍介於 \(0\) 和 \(\frac{1}{2}\pi\) 之間。這將給我們更新後的反射積分：

\[ L_o(p,\phi_o, \theta_o) = k_d\frac{c}{\pi} \int_{\phi = 0}^{2\pi} \int_{\theta = 0}^{\frac{1}{2}\pi} L_i(p,\phi_i, \theta_i) \cos(\theta) \sin(\theta) d\phi d\theta \]

求解這個積分需要我們在半球 \(\Omega\) 內取得固定數量的離散樣本，並將其結果平均。根據黎曼和的原理，這將積分轉換為以下離散版本，其中在每個球座標上分別有 \(n1\) 和 \(n2\) 個離散樣本：

\[ L_o(p,\phi_o, \theta_o) = k_d \frac{c\pi}{n1 n2} \sum_{\phi = 0}^{n1} \sum_{\theta = 0}^{n2} L_i(p,\phi_i, \theta_i) \cos(\theta) \sin(\theta) d\phi d\theta \]

如同前一張圖所示，由於我們對兩個球座標值都進行了離散採樣，每個樣本都會近似或平均半球上的一個區域。請注意，由於球體的一般特性，天頂角 \(\theta\) 越高，半球的離散採樣區域就越小，因為採樣區域會向中心頂部匯聚。為了補償較小的區域，我們透過將面積乘以 \(\sin \theta\) 來加權其貢獻。

給定積分的球座標，對半球進行離散採樣，轉換為以下片元程式碼：

vec3 irradiance = vec3(0.0);

vec3 up    = vec3(0.0, 1.0, 0.0);
vec3 right = normalize(cross(up, normal));
up         = normalize(cross(normal, right));

float sampleDelta = 0.025;
float nrSamples = 0.0;
for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
{
    for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
    {
        // spherical to cartesian (in tangent space)
        vec3 tangentSample = vec3(sin(theta) * cos(phi),  sin(theta) * sin(phi), cos(theta));
        // tangent space to world
        vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N;

        irradiance += texture(environmentMap, sampleVec).rgb * cos(theta) * sin(theta);
        nrSamples++;
    }
}
irradiance = PI * irradiance * (1.0 / float(nrSamples));

我們指定了一個固定的 sampleDelta 增量值來遍歷半球；減小或增加採樣增量將分別增加或減少準確性。

在兩個迴圈中，我們取用這兩個球座標，將它們轉換為 3D 笛卡爾採樣向量，再將樣本從切線空間轉換為圍繞法線定向的世界空間，並使用這個採樣向量直接採樣 HDR 環境貼圖。我們將每個採樣結果加到 irradiance 中，最後再除以總採樣數，得到平均採樣輻照度。請注意，由於光線在較大角度時會較弱，我們將採樣顏色值乘以 cos(theta)；又因為半球較高區域的採樣面積較小，我們將其乘以 sin(theta) 來進行補償。

現在剩下的工作就是設定 OpenGL 的渲染程式碼，以便我們可以對前面捕捉到的 envCubemap 進行卷積。首先，我們創建輻照度立方體貼圖（同樣，我們只需在渲染迴圈之前執行一次即可）：

unsigned int irradianceMap;
glGenTextures(1, &irradianceMap);
glBindTexture(GL_TEXTURE_CUBE_MAP, irradianceMap);
for (unsigned int i = 0; i < 6; ++i)
{
    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 32, 32, 0,
                 GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

由於輻照度圖會均勻地平均所有周圍的輻射，它沒有太多高頻細節，所以我們可以將貼圖儲存在較低解析度（32x32），並讓 OpenGL 的線性過濾來完成大部分工作。接下來，我們將捕捉幀緩衝區重新調整到新的解析度：

glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 32, 32);

使用卷積著色器，我們以類似於捕捉環境立方體貼圖的方式來渲染環境貼圖：

irradianceShader.use();
irradianceShader.setInt("environmentMap", 0);
irradianceShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);

glViewport(0, 0, 32, 32); // don't forget to configure the viewport to the capture dimensions.
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
for (unsigned int i = 0; i < 6; ++i)
{
    irradianceShader.setMat4("view", captureViews[i]);
    glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0,
                           GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, irradianceMap, 0);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

    renderCube();
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);

現在，在這個流程之後，我們應該有了一個預運算的輻照度圖，可以直接用於我們的漫射基於圖片的光照。為了檢查我們是否成功對環境貼圖進行了卷積，我們將用輻照度圖取代環境貼圖作為天空盒的環境採樣器：

如果它看起來像是環境貼圖的高度模糊版本，那恭喜你，你已經成功地對環境貼圖進行了卷積。

PBR 與間接輻照度光照

輻照度圖代表了反射積分中，由所有周圍間接光累積而來的漫射部分。由於光線並非來自直接光源，而是來自周圍環境，我們將漫射和鏡面反射的間接光照都視為環境光照，取代我們之前設定的常數項。

首先，請務必將預先計算好的輻照度圖新增為一個立方體採樣器：

uniform samplerCube irradianceMap;

鑑於輻照度圖包含了場景中所有的間接漫射光，要取得影響片元的輻照度，只需使用表面法線進行一次紋理採樣即可：

// vec3 ambient = vec3(0.03);
vec3 ambient = texture(irradianceMap, N).rgb;

然而，由於間接光照同時包含漫射和鏡面反射部分（正如我們從反射方程式的拆分版本中所看到的），我們需要據此來權衡漫射部分的比例。與我們在上一章節所做的一樣，我們使用菲涅爾方程式來決定表面的間接反射率，再從中得出折射（或漫射）率：

vec3 kS = fresnelSchlick(max(dot(N, V), 0.0), F0);
vec3 kD = 1.0 - kS;
vec3 irradiance = texture(irradianceMap, N).rgb;
vec3 diffuse    = irradiance * albedo;
vec3 ambient    = (kD * diffuse) * ao;

由於環境光來自圍繞法線 N 定向的半球內的所有方向，因此沒有單一的半向量（halfway vector）可以決定菲涅爾響應。為了仍然能模擬菲涅爾效應，我們根據法線和視圖向量之間的夾角來計算菲涅爾。然而，早些時候我們將受表面粗糙度影響的微平面半向量作為菲涅爾方程式的輸入。由於我們目前沒有考慮粗糙度，表面的反射率總是會相對較高。間接光遵循與直接光相同的屬性，因此我們預期較粗糙的表面在邊緣處的反射會較弱。正因如此，間接菲涅爾反射強度在粗糙的非金屬表面上看起來會不太對勁（為了演示目的而稍微誇大）：

我們可以透過在菲涅爾-施利克（Fresnel-Schlick）方程式中，注入一個粗糙度項來緩解這個問題，這個方法由 Sébastien Lagarde 所描述：

vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness)
{
    return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(clamp(1.0 - cosTheta, 0.0, 1.0), 5.0);
}

透過在計算菲涅爾響應時將表面的粗糙度納入考量，環境光程式碼最終變為：

vec3 kS = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);
vec3 kD = 1.0 - kS;
vec3 irradiance = texture(irradianceMap, N).rgb;
vec3 diffuse    = irradiance * albedo;
vec3 ambient    = (kD * diffuse) * ao;

如你所見，實際的基於圖片的光照計算非常簡單，只需要一次立方體貼圖的紋理查詢；大部分的工作都在於預運算或對輻照度圖進行卷積。

如果我們拿 PBR 光照章節中的初始場景，其中每個球體的金屬度從上到下遞增，粗糙度從左到右遞增，並加入漫射的基於圖片的光照，它會看起來有點像這樣：

畫面看起來還是有點奇怪，因為金屬度越高的球體需要某種形式的反射才能看起來像真正的金屬表面（因為金屬表面不反射漫射光），而目前這些反射只來自於（微弱的）點光源。儘管如此，你已經可以感覺到這些球體在環境中顯得更「協調」（特別是如果你切換不同的環境貼圖），因為表面反應會根據環境的環境光照做出相應的變化。

你可以在這裡找到所有討論主題的完整原始碼。在下一個章節中，我們將加入反射積分的間接鏡面反射部分，屆時我們將會真正見識到 PBR 的強大威力。

第四十二章