第十章

开始 • 相機

發布時間：2025-06-14 閱讀時間：41 分鐘

譯者歸納：這篇講解了 3D 世界中相機的概念。這個概念是自然而然推進的，絕非胡亂製造的新概念。在 OpenGL 的渲染中，本身就已經有了相機的影子。相機是什麼？相機是一個設備，它讓世界萬物得以呈現，否則還能怎麼辦呢？閉著眼睛遐想嗎？在 3D 世界中，物件本身是客觀存在的，這是我們人類大腦的固有構造，它自然而然就是那個樣子的。我們根據這個固有的觀念去構建一個虛擬世界（由頂點、顏色、混合、遮擋、陰影等組成），將數據放置於特定空間中，然後使用「渲染 (render)」邏輯處理這個虛擬世界。透過鏡頭，我們看見它，這就是它的樣子，讓我們彷彿置身一個現實世界裡（為什麼？因為我們就是按照眼睛感知世界的方式去模仿的！）。

上一章，我們討論了 view 矩陣以及如何使用它來移動場景（我們向後移動了一些），OpenGL 自己並不清楚相機這個概念，但是我們可以嘗試模擬一個，方式是使場景裡的所有物件反方向移動，這給了用戶一種幻覺——是我們自己在移動。

這一章，我們將討論如何在 OpenGL 裡配置相機。我們將討論 fly 風格的相機，它讓你在 3D 場景裡自由地移動。我們也將討論鍵盤和鼠標輸入，最後我們會完成一個相機類（class）。

相機/視圖空間

當我們在談論相機/視圖空間的時候，我們談論的是所有的頂點座標，那些我們能夠以相機視角——作為場景的中心——看見的頂點座標：此視圖矩陣將全體世界座標轉換為視圖空間座標，即相對相機之位置、朝向。欲定義一個相機，我們需要其在世界的位置，以其所看之方向，一個指向其右側的向量，一個指向其上方的向量。細心讀者或許注意到，我們實際上正創建一個座標系統，憑藉的是 3 個正交的單位軸，相機位置作為原點。

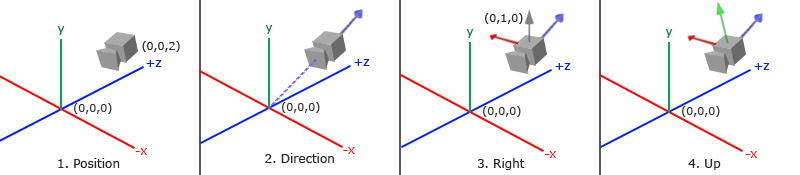
1. 相機位置

獲取相機位置容易。位置是一個向量，它處於世界空間，指向相機的位置。我們將相機置於此前所放之位置：

glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);

莫忘 z 軸正向乃穿透屏幕指向你，因此若我們要後移相機，沿 z 軸正向即可。

2. 相機方向

此後所需之向量，乃相機之方向，即相機所指。此時，我們令其指向場景之中心 $(0,0,0)$。記得否，如對二向量行減法，所得是二者之差？故，對相機位置及場景之中心行減法，所得正是我們想要的那個向量：相機方向。至於視圖矩陣所含之座標系統，我們將置其 z 軸為正，因就 OpenGL 慣例所言，相機指向 z 軸之負向，我們將其方向向量施 negate 操作。如將上述減法中二向量順序調換，我們將得到一個指向相機 z 負軸的向量。

glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);

此處，名稱“方向向量”非最好的名字，因為它實際上指向的是相機所看目標之反方向。

3. Right 軸 （Right axis）

此後所需向量，乃 Right 向量，亦即相機空間的 x 正向。欲取得此向量，我們使用一個小技巧，其中我們會首先確定一個 Up 向量，一個相對世界空間指向相機上方的向量。然後，我們對 Up 向量和 Direction 向量執行叉積計算。由於叉積的結果是一個對二向量都正交的向量，我們將得到一個指向 x 軸正方向的向量（如果我們交換叉積算子的順序，我們將得到一個指向 x 軸負向的向量）：

glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));

4. Up 軸

現在，我們有了 x 軸以及 z 軸，要獲得相機的 y 軸就相對容易了，我們對 Right 向量和 Direction 向量執行叉積計算：

glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);

得益於叉積法則，及幾個小技巧，我們能夠得到構建相機空間所需的全部向量。對數學有熱情的讀者，這個過程在線性代數，被稱為 Gram-Schmidt 計算。使用相機的這些向量，我們現在可以創建 LookAt 矩陣，事實上，它對於相機的創建非常有用！

Look At

矩陣有個有趣的特點，當你定義了 3 個相互正交的（或者叫做非線性）軸，使用此三軸外加一個平移向量，你創建出一個矩陣，由這個矩陣，可以通過“矩陣-向量”乘法，將任意向量轉入由這“3 個軸 - 1 個平移向量”定義的座標空間。

LookAt = \begin{bmatrix} \color{red}{R_x} & \color{red}{R_y} & \color{red}{R_z} & 0 \\ \color{green}{U_x} & \color{green}{U_y} & \color{green}{U_z} & 0 \\ \color{blue}{D_x} & \color{blue}{D_y} & \color{blue}{D_z} & 0 \\ 0 & 0 & 0  & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & -\color{purple}{P_x} \\ 0 & 1 & 0 & -\color{purple}{P_y} \\ 0 & 0 & 1 & -\color{purple}{P_z} \\ 0 & 0 & 0  & 1 \end{bmatrix}

其中 $\color{red}{R}$ 是 Right 向量，$\color{green}{U}$ 是 Up 向量，$\color{blue}{D}$ 是 Direction 向量，$\color{purple}{P}$ 是相機的位置向量。注意旋轉（左矩陣）以及平移（右矩陣）部分被反轉了（分別被 transposed 和 negated），這是因為，我們希望以與相機運動相反的方向旋轉和移動場景（世界）。將這個 LookAt 矩陣作為我們的視圖矩陣，剛好可以將全部的世界座標轉入我們方才定義的相機空間。LookAt 矩陣準確地表述了它的目的：它創建一個視圖矩陣，使看向指定的目標。

有幸，GLM 已幫助我們做了全部工作。我們只需指定相機位置，一個目標位置以及一個在世界空間的 Up 向量（我們使用它來計算 Right 向量）。GLM 然後創建 LookAt 矩陣，也就是我們的視圖矩陣：

glm::mat4 view;
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),
  		   glm::vec3(0.0f, 0.0f, 0.0f),
  		   glm::vec3(0.0f, 1.0f, 0.0f));

glm::LookAt 函數需要一個位置、目標以及一個 up 向量。這個例子創建了一個視圖矩陣，和上一章我們創建過的那個是一樣的。

在探索“用戶輸入”之前，我們來一點有趣的玩法，首先我們繞著世界轉動我們相機。我們將目標固定在 (0,0,0)。使用一點三角函數的知識，在每一幀創建一個 x 和 z 座標，它們分別表示一個“圓”上的點，我們將會把這個“點”設為相機的位置。通過再次計算 x 和 y 座標，我們對圓上的每個點進行遍歷，於是，相機就會繞著場景（世界）旋轉。爾通過定義好的半徑 radius，我們在每一幀對這個圓擴大處理，繼而創建一個新的視圖矩陣，這裡我們使用的 GLFW 的 glfwGetTime 函數獲取時間：

const float radius = 10.0f;
float camX = sin(glfwGetTime()) * radius;
float camZ = cos(glfwGetTime()) * radius;
glm::mat4 view;
view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::vec3(0.0, 1.0, 0.0));

如果你的代碼跑起來，應該得到這樣的結果：

使用這一小段代碼，相機現在圍繞場景不斷轉圈。儘管去嘗試修改半徑和位置/方向等參數，這樣你就可以感知 LookAt 到底是如何工作的。同時，如果你遇到阻礙，也可以查閱源代碼。

散步（Walk around）

使相機繞場景旋轉很有趣，然而更有趣的是讓相機的運動受我們控制！首先我們需要設置一個相機系統，如此，在程序的最開始定義一些相機參數會非常有用：

glm::vec3 cameraPos   = glm::vec3(0.0f, 0.0f,  3.0f);
glm::vec3 cameraFront = glm::vec3(0.0f, 0.0f, -1.0f);
glm::vec3 cameraUp    = glm::vec3(0.0f, 1.0f,  0.0f);

LookAt 函數現在是這樣：

view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);

首先，我們設置相機的位置為方才定義的 cameraPos。方向是當前位置加上方才定義的 Direction 向量。這可以確保不管我們如何移動，相機始終看向目標。當我們按下某些鍵的時候，我們通過修改 cameraPos 向量來把玩一下。

我們已經定義了函數 processInput，它用於管理 GLFW 的鍵盤輸入，讓我們加入幾個額外的按鍵命令：

void processInput(GLFWwindow *window)
{
    ...
    const float cameraSpeed = 0.05f; // adjust accordingly
    if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
        cameraPos += cameraSpeed * cameraFront;
    if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
        cameraPos -= cameraSpeed * cameraFront;
    if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
        cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
    if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
        cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
}

當我們按下 WASD 的任意一個鍵的時候，相機的位置會被相應改變。如果我們想向前或者向後移動，我們對相機 位置向量 加或者減 這個方向向量 * 一個移動速度標量。如果我們希望向兩側移動相機，使用叉積創建一個 Right 向量，然後我們沿著這個向量移動一個距離。這會在使用攝影機時產生熟悉的平移（Strafe）效果。

注意，我們對最後的 Right 向量進行了標準化。如果我們沒有這樣做，最後叉積返回的結果會由 cameraFront 變量決定，在 size 上稍稍不同。缺少了標準化這一步，我們移動的速度會根據相機的朝向時快時慢，而非平緩。

此時，你應該已經能夠讓攝影機稍微移動了，儘管速度會因系統而異，因此你可能需要調整 cameraSpeed。

移動速度

目前我們使用一個常量來控制相機移動速度。理論上這似乎沒啥問題，但是實際上，用戶電腦的處理能力、結果會稍稍存在差異，有些電腦每秒可以渲染更多的幀數。一旦用戶電腦單秒渲染幀數較多，其接收輸入也會更頻繁。結果就是有些用戶移動得快，爾有些移動得慢，取決於他們的配置。當發布應用的時候，你一定希望確保其運行效果在所有硬件上一致。

圖形應用和遊戲常常跟蹤 deltaTime 這個變量，它保存了上一幀花銷的時間。我們使用它乘以所有的速度值。結果就是，當 deltaTime 的值很大，就意味著上一幀花銷的時間長於平均值，那麼可以讓這時的速度稍微快一點，以達到整體的平衡。當使用此辦法，電腦處理快慢就無所謂了，相機速度也會根據用戶設備相應地做出平衡調整，從而使我們獲得一致的體驗。

為了計算 deltaTime，我們跟蹤 2 個全局變量：

loat deltaTime = 0.0f;	// Time between current frame and last frame
float lastFrame = 0.0f; // Time of last frame

接下來，在幀內，我們計算最新的 deltaTime 值，以作後續之用：

float currentFrame = glfwGetTime();
deltaTime = currentFrame - lastFrame;
lastFrame = currentFrame;

現在，我們有了 deltaTime，我們可以在計算速度的時候將它納入考慮：

void processInput(GLFWwindow _window)
{
float cameraSpeed = 2.5f _ deltaTime;
[...]
}

由於我們使用了 deltaTime，相機將以一個均衡的速度移動，其值為每秒 2.5 個單位。結合上一章，我們現在應該獲得了一個非常流暢的、非常穩定的相機系統，我們用它來環繞整個場景：

現在，我們的相機在任何系統上運行速度都大概一樣。還是老規矩，看一下源代碼，如果有困難的話。我們將看到，但凡涉及運動問題， deltaTime 也會常常伴隨它出現。

環視（Look around）

僅僅使用鍵盤來實現四處移動並不那麼有趣。特別是，我們無法轉向，這使移動非常受限。於是，鼠標的作用可以派上用場了！

要實現場景內環視，我們必須修改向量 cameraFront，可以根據鼠標輸入進行。但基於鼠標的轉動來修改方向向量有點複雜，需要一點三角幾何知識。如果你不懂三角幾何，不要怕，你可以放心跳過閱讀其中的代碼部分，將它們複製到你的項目裡即可。你可以隨時回來閱讀，如果你想了解更多。

歐拉角 （Euler angles）

歐拉角由三個數值組成，它可以表達 3D 場景下的任意旋轉。它由 Leonhard Euler 於 1700 年代定義。有 3 個歐拉角度：pitch、yaw 和 roll。下面這個圖給了你它們的視覺含義：

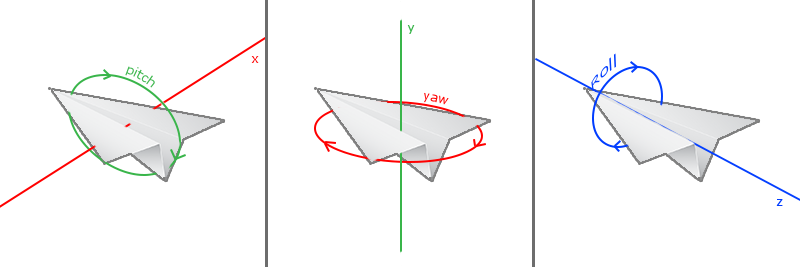
pitch 表達的是我們在“上下”方向轉動的量，如上方第一張圖所示。第二張圖展示了 yaw 的值，它表達的是“左右”方向轉動的量。roll 意指繞相機鏡頭朝向轉動的量，它經常用於空間飛行相機。歐拉角的每個分量都代表一個角度，將它們三個組合起來，我們就可以計算 3D 空間中的任意旋轉向量。

對於我們的相機系統，我們只關心 yaw 和 pitch，因此我們無需討論 roll。給定 yaw 和 pitch，我們就可以將它們轉換為一個 3D 向量，它意指一個新的方向向量。將 yaw 和 pitch 轉為方向向量的過程需要一點三角幾何知識，我們以一個基礎的例子開始吧：

讓我們先來稍微複習一下，並檢查一下一般的直角三角形情況（其中一邊是 90 度的角）。

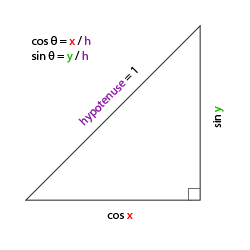
如果我們將斜邊長度定義為 1，我們由三角函數（soh cah toa）知道其鄰邊長度是 ${\cos{x/h}=\cos{x/1}=\cos{x}}$，爾其對邊長度是 $\sin{y/h}=\sin{y/1}=\sin{y}$。這給了我們一種通用公式，對於直角三角形情況，給定其中一個角度，可以由此得到 x 和 y 邊的長度。讓我們使用它計算出方向向量的分量。

讓我們設想一個同樣的三角形，但是我們從正上方視角去觀察它，使它的鄰邊和對邊分別和場景的 x 和 z 軸平行（就像從 y 軸看過去）。

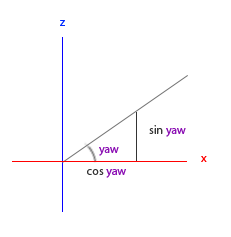
如果我們以逆時針方向，並從 x 軸開始，對 yaw 角進行可視化，我們會看到其三角形的 x 邊長度和 $\cos(yaw)$ 相關。類似，z 邊的長度和 $\sin(yaw)$ 相關。

那麼，使用這個知識，給定 yaw 值之後，我們可以用它來創建相機的方向向量：

glm::vec3 direction;
direction.x = cos(glm::radians(yaw)); // Note that we convert the angle to radians first
direction.z = sin(glm::radians(yaw));

這解決了我們如何通過一個 yaw 值得到一個 3D 方向向量的問題。然而，pitch 也需要被考慮。讓我們現在看向 y 軸，就像我們坐在 xz 平面一樣：

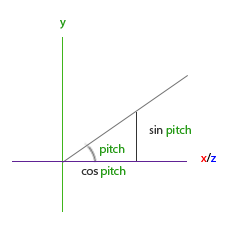
類似，由這個三角形，我們可以看到方向的 y 分量等於 $\sin(pitch)$，因此，讓我們將其寫入：

direction.y = sin(glm::radians(pitch));

然而，由 pitch 三角形，我們也知道 xz 邊會被 $\cos(pitch)$ 影響，因此我們需要確保它也是方向向量的一部分。考慮這些之後，我們得到了最終的方向向量，它們由 yaw 和 pitch 歐拉角翻譯得來：

direction.x = cos(glm::radians(yaw)) _ cos(glm::radians(pitch));
direction.y = sin(glm::radians(pitch));
direction.z = sin(glm::radians(yaw)) _ cos(glm::radians(pitch));

這給了我們一個公式，由它，我們可以將 yaw 和 pitch 轉為一個 3D 方向向量，使用它，我們可以環視整個場景。

我們已經將場景配置為，使全部物件置於 z 軸的負方向。然而，如果我們觀察 X 和 Z 軸的偏航（yaw）三角形，我們會發現，當 θ 為 0 時，攝像機的朝向向量會指向正 X 軸。要使相機指向 z 軸負方向，我們可以將 yaw 的默認值設置為順時針 90 度。正值會導致逆時針旋轉，因此，我們將 yaw 的默認值設置為：

yaw = -90.0f;

到此，你或許疑惑：我們該如何設置和修改 yaw 和 pitch 值呢？

鼠標輸入

yaw 和 pitch 的值來自鼠標移動，其中水平移動影響的是 yaw，爾垂直移動影響的是 pitch。其思想是，保存上一幀的鼠標位置，並在當前幀計算鼠標移動了多少。移動的越多，pitch 和 yaw 值就會改變越多，因此我們相機也會移動更多。

首先，我們將告訴 GLFW 隱藏光標，並捕獲它。“捕獲它”的意思是，一旦應用獲取了焦點，光標就停留在窗口的中心（除非應用失焦或者推出）。我們可以通過一個簡單的配置函數達到此目的：

glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED);

這樣調用之後，不管我們如何移動鼠標，光標都不可見，並且不離開窗口。這對於一個 FPS（第一人稱射擊類）相機系統是完美的。

要計算 pitch 和 yaw，我們需要告訴 GLFW 監聽鼠標移動事件。我們通過創建一個如下形式的回調函數實現它：

void mouse_callback(GLFWwindow* window, double xpos, double ypos);

這裡，xpos 和 ypos 代表了當前鼠標的位置。一旦我們使用 GLFW 註冊了這個回調函數，那麼在每一幀，當鼠標有移動的時候，mouse_callback 函數都會被調用：

glfwSetCursorPosCallback(window, mouse_callback);

當為 fly 風格的相機處理鼠標輸入的時候，有若干步驟需要我們去完成，這樣我們才能完整的計算出相機的 Direction 向量：

1. 計算上一幀鼠標的偏移量 （offset）
2. 將 offset 加到相機的 yaw 和 pitch 值
3. 補充一些最小/最大 pitch 值約束
4. 計算方向

第一步是計算上一幀的 offset。我們先將上一幀的鼠標位置保存下來，我們將它初始化在屏幕（屏幕大小為 800✖️600）的中心：

float lastX = 400, lastY = 300;

然後，在鼠標回調函數，我們計算 offset：

float xoffset = xpos - lastX;
float yoffset = lastY - ypos; // reversed since y-coordinates range from bottom to top
lastX = xpos;
lastY = ypos;

const float sensitivity = 0.1f;
xoffset *= sensitivity;
yoffset *= sensitivity;

注意，我們對 offset 乘以一個敏感度。如果我們忽略了這個事情，那麼鼠標的移動將會非常強烈；你可以根據你的喜好調整敏感度。

接下來，將 offset 加到全局的 pitch 和 yaw 值：

yaw   += xoffset;
pitch += yoffset;

第三步中，我們要加點約束，這樣用戶就不會搞出一些奇怪的移動操作（當朝向向量與世界坐標系的向上方向平行時，也會導致 LookAt 函數出現翻轉）。pitch 需要以以上方式限制其大小，如此用戶才不至於看向 89 度以上的方向（在 90 度的地方，我們的 LookAt 會產生翻轉）並且也不能看向低於 -89 度的方向。這可以保證用戶能夠看到天空以及自己的腳，但是不能再進一步了。這個約束的實現辦法是，在角度超過約束值的時候，將歐拉角替換以約束值。

if(pitch > 89.0f)
  pitch =  89.0f;
if(pitch < -89.0f)
  pitch = -89.0f;

注意，我們沒有對 yaw 實施約束，因為我們不希望對用戶的水平轉動加以約束。然而，要對 yaw 加約束，和對 pitch 加約束一樣簡單。

最後一步，計算相機的方向向量，我們使用上一部分裡得到的公式：

glm::vec3 direction;
direction.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));
direction.y = sin(glm::radians(pitch));
direction.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));
cameraFront = glm::normalize(direction);

計算出的方向會包含全部的旋轉信息，爾它是由鼠標的移動算出來的。由於 cameraFront 已經包含在 glm 的 lookat 函數裡，我們直接開始就好了。

如果運行代碼，你會發現，每次窗口第一次接收到焦點的時候，相機有一個很大的跳躍。這個跳躍的成因在於，一旦你的光標進入窗口，鼠標回調函數接收到的 xpos 和 ypos 等於你的鼠標進入屏幕的位置。這個位置常常遠離屏幕的中心，從而導致了一個比較大的偏移，也因此產生了鼠標移動的跳躍。我們可以通過定義一個全局變量，用於判斷是否首次接收鼠標輸入，並以此避免這個問題。如果是第一次，我們將鼠標的位置初始化為新的 xpos 和 ypos。這樣以來，鼠標移動將使用新設置的鼠標移入時位置來進行 offset 的計算：

if (firstMouse) // initially set to true
{
    lastX = xpos;
    lastY = ypos;
    firstMouse = false;
}

最終的代碼變為這樣：

void mouse_callback(GLFWwindow* window, double xpos, double ypos)
{
    if (firstMouse)
    {
        lastX = xpos;
        lastY = ypos;
        firstMouse = false;
    }

    float xoffset = xpos - lastX;
    float yoffset = lastY - ypos;
    lastX = xpos;
    lastY = ypos;

    float sensitivity = 0.1f;
    xoffset *= sensitivity;
    yoffset *= sensitivity;

    yaw   += xoffset;
    pitch += yoffset;

    if(pitch > 89.0f)
        pitch = 89.0f;
    if(pitch < -89.0f)
        pitch = -89.0f;

    glm::vec3 direction;
    direction.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));
    direction.y = sin(glm::radians(pitch));
    direction.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));
    cameraFront = glm::normalize(direction);
}

好了！旋轉一下，你將看到我們限制可以在 3D 場景裡自由移動了！

推拉鏡頭（Zoom）

作為相機系統的一點補充，我們將實現 zooming 交互接口。上一章裡，我們說過，視野或者 fov 定義了我們能看到場景範圍。當 fov 變小，場景映射的空間也會變小。在同樣的 NDC 空間下，更小的映射可以給用戶一種拉進鏡頭的感覺。要拉進鏡頭，我們將使用鼠標的滾輪。和鼠標的移動以及鍵盤輸入類似，我們有一個針對鼠標滾動的回調函數：

void scroll_callback(GLFWwindow* window, double xoffset, double yoffset)
{
    fov -= (float)yoffset;
    if (fov < 1.0f)
        fov = 1.0f;
    if (fov > 45.0f)
        fov = 45.0f;
}

當滾動的時候，yoffset 值告訴我們在垂直方向上滾動了多少。當 scroll_callback 函數被調用，我們修改全局定義的 fov 值。由於 45.0 是默認的 fov 值，我們希望將 zoom 等級約束在 1.0 到 45.0 之間。

現在，我們必須於每一幀上傳此透視投影矩陣至 GPU。不過這一次，我們使用一個 fov 變量作為視野：

projection = glm::perspective(glm::radians(fov), 800.0f / 600.0f, 0.1f, 100.0f);

最後，不要忘了註冊 scroll 回調函數：

glfwSetScrollCallback(window, scroll_callback);

你做到了！我們實現了一個簡單的相機系統，它允許我們在 3D 環境裡自由移動。

大膽去玩這些代碼！如果你遇到困難，那就和源代碼對照一下。

相機類（Camera Class）

在接下來的章節中，我們將始終使用一個攝像機，以便輕鬆地在場景中四處查看，並從各個角度觀察結果。然而，由於相機代碼會佔用很大篇幅，我們將對其中的細節進行抽象，並實現一個我們自己的相機對象，附加一些使用特性，它可以應付大部分工作。不像 Shader 那一章，我們不準備展開相機類的編寫過程；但是，如果你希望了解內部實現，我們會將其（附有完整的注釋）源代碼提供給你。

就像 Shader 對象，我們將相機類完全定義在一個 header 文件裡。你可以在這裡找到它；這一章讀完，你應該可以理解其中的代碼了。非常建議，最少將代碼讀一次，以作為你可以創建自己的相機系統的一個例證。

我們介紹的相機系統是類 fly 風格相機，它適用於大部分場景，對歐拉角非常友好。但是，要注意的時候，當創建不同的相機系統，比如一個 FPS 相機，或者一個飛行模擬相機，每一個相機系統有它自己的優點和缺點。正因此，你一定要去好好讀一下相關解釋或說明。比如説，我們的 fly 相機不允許 pitch 到 90 或者 90 度以上，將 Up 向量設置為 (0,1,0) 是不會產生實際作用的，當考慮到到 roll 值。

包含此相機類的源代碼的更新版本可以在這裡找到。

• 1. 介绍
• 2. 开始 • 认识 OpenGL
• 3. 开始 • 创建一个窗口
• 4. 开始 • Hello, 窗口
• 5. 开始 • Hello, 三角形
• 6. 开始 • 著色器
• 7. 开始 • 紋理
• 8. 开始 • 轉換
• 9. 开始 • 座標系統
• 10. 开始 • 相機
• 11. 光 • 顏色
• 12. 光 • 基本光照
• 13. 光 • 材質
• 14. 光 • 光照貼圖
• 15. 光 • 光源
• 16. 光 • 多重光源
• 17. 模型載入 • Assimp
• 18. 模型載入 • Mesh
• 19. 模型載入 • Model
• 20. 高級 OpenGL • 深度測試
• 21. 高級 OpenGL • 模板測試
• 22. 高級 OpenGL • 混合
• 23. 高級 OpenGL • 面剔除
• 24. 高級 OpenGL • Framebuffers
• 25. 高級 OpenGL • Cubemaps
• 26. Advanced-OpenGL • Advanced-Data
• 27. Advanced-OpenGL • Advanced-GLSL
• 28. Advanced-OpenGL • Instancing
• 29. Advanced-OpenGL • Anti-Aliasing
• 30. 高級光照
• 31. 高級光照 • 伽馬矯正
• 32. 高級光照 • Shadow-Mapping
• 33. Advanced-Lighting • Point-Shadows
• 34. 高級光照 • 法線貼圖 (Normal Mapping)
• 35. 高級光照 • 視差貼圖（Parallax Mapping）
• 36. 高級光照 • HDR
• 37. 高級光照 • 輝光（Bloom）
• 38. 高級光照 • 延遲著色
• 39. 高級光照 • SSAO