第四十三章

PBR • Specular-IBL

發布時間：2025-08-04 閱讀時間：62 分鐘

在前一個章節中，我們透過預先計算輻射度圖（irradiance map），作為照明的間接漫射部分，來結合基於圖像的光照（IBL）設定 PBR。在這個章節中，我們將專注於反射方程式的鏡面反射部分：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

你會注意到 Cook-Torrance 的鏡面反射部分（乘以 \(kS\)）在積分中並不是常數，它取決於入射光方向，也取決於入射視線方向。試圖針對所有入射光方向，以及所有可能的視線方向，來解這個積分會造成組合爆炸（combinatorial overload），並且在即時運算中成本過高。Epic Games 提出了一個解決方案，他們在做出一些妥協的情況下，能夠為即時運算預先卷積（pre-convolute）鏡面反射部分，這個方法被稱為「split sum approximation」（分離求和近似）。

分離求和近似將反射方程式的鏡面反射部分分成兩個獨立的部分，我們可以分別對這兩個部分進行卷積，然後在 PBR shader 中結合它們，以實現鏡面反射的間接圖像光照（specular indirect image based lighting）。與我們預先卷積輻射度圖的方式類似，分離求和近似也需要一個 HDR 環境貼圖作為其卷積輸入。為了理解分離求和近似，我們將再次檢視反射方程式，但這次只專注於鏡面反射部分：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)} L_i(p,\omega_i) n \cdot \omega_i d\omega_i = \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

和輻射度卷積一樣，出於效能考量，我們不能在即時運算中求解積分的鏡面反射部分，還期望有合理的效能。因此，我們最好預先計算這個積分，得到一個類似於鏡面反射 IBL 貼圖的東西，然後用片段的法線對這個貼圖進行取樣，大功告成。然而，這就是有點棘手的地方。我們之所以能預先計算輻射度圖，是因為積分只取決於 \(\omega_i\) ，並且我們可以將常數的漫射反照率（albedo）項移到積分外面。但這次，從 BRDF 可以明顯看出，積分不僅僅取決於 \(\omega_i\) ：

\[ f_r(p, w_i, w_o) = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)} \]

積分也取決於 \(w_o\)，而我們無法用兩個方向向量對預先計算的立方體貼圖進行取樣。上一章節有提過，位置 \(p\) 在這裡不重要。在即時運算中，針對 \(\omega_i\) 和 \(\omega_o\) 的每一種可能組合預先計算這個積分是不切實際的。

Epic Games 的分離求和近似透過將預先計算拆分成兩個獨立的部分，解決了這個問題，我們之後可以將它們結合起來，得到我們所追求的預先計算結果。分離求和近似將鏡面反射積分拆分為兩個獨立的積分：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} L_i(p,\omega_i) d\omega_i * \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i \]

第一個部分（進行卷積後）被稱為「pre-filtered environment map」（預過濾環境貼圖），它（與輻射度圖類似）是一個預先計算的環境卷積貼圖，但這次考慮了粗糙度（roughness）。對於增加的粗糙度等級，環境貼圖會與更分散的取樣向量進行卷積，產生更模糊的反射。對於我們進行卷積的每一個粗糙度等級，我們會將依序模糊的結果儲存在預過濾貼圖的 mipmap 等級中。舉例來說，一個將 5 個不同粗糙度值的預卷積結果儲存在其 5 個 mipmap 等級中的預過濾環境貼圖，看起來會像這樣：

我們使用 Cook-Torrance BRDF 的常態分佈函數（NDF）來生成取樣向量及其分散程度，該函數將法線和視線方向作為輸入。由於我們在對環境貼圖進行卷積時事先不知道視線方向，Epic Games 做了進一步的近似，假設視線方向（以及鏡面反射方向）等於輸出取樣方向 \(\omega_o\) 。這轉化為以下程式碼：

vec3 N = normalize(w_o);
vec3 R = N;
vec3 V = R;

這樣一來，預過濾環境卷積就不需要知道視線方向了。不過這確實意味著，當我們從某個角度觀察鏡面反射表面時，無法獲得漂亮的擦地鏡面反射（grazing specular reflections），如下圖所示（圖片來自《Moving Frostbite to PBR》文章）；然而，這通常被認為是可接受的妥協：

分離求和方程式的第二部分等於鏡面反射積分的 BRDF 部分。如果我們假設入射輻射（incoming radiance）對於每個方向都是完全白色的（因此 \(L(p, x) = 1.0\)），我們可以預先計算 BRDF 的反應，給定一個輸入粗糙度以及法線 \(n\) 和光線方向 \(\omega_i\) 之間的輸入角度，或者說 \(n \cdot \omega_i\) 。Epic Games 將預先計算的 BRDF 對於每個法線和光線方向組合，在不同的粗糙度值下的反應，儲存在一個二維的查詢貼圖（lookup texture，簡稱 LUT）中，這個貼圖被稱為「BRDF integration」圖。這個二維查詢貼圖會輸出一個縮放值（紅色）和一個偏移值（綠色），給表面的菲涅爾（Fresnel）反應，這就給了我們分離鏡面反射積分的第二部分：

我們生成查詢貼圖的方式是，將一個平面的水平紋理座標（範圍介於 0.0 和 1.0 之間）視為 BRDF 的輸入 \(n \cdot \omega_i\) ，並將其垂直紋理座標視為輸入的粗糙度值。有了這個 BRDF 整合圖和預過濾環境貼圖，我們就可以將兩者結合起來，得到鏡面反射積分的結果：

float lod             = getMipLevelFromRoughness(roughness);
vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
vec2 envBRDF          = texture2D(BRDFIntegrationMap, vec2(NdotV, roughness)).xy;
vec3 indirectSpecular = prefilteredColor * (F * envBRDF.x + envBRDF.y)

這應該能讓您對 Epic Games 的分離求和近似，如何大致處理反射方程式的間接鏡面反射部分，有一個概觀。現在讓我們試著自己建構這些預卷積的部分。

預過濾 HDR 環境貼圖

預過濾環境貼圖與我們對輻射度圖進行卷積的方式非常相似。不同之處在於，我們現在要考慮粗糙度，並將依序更粗糙的反射結果儲存在預過濾貼圖的 mip 層級中。

首先，我們需要生成一個新的立方體貼圖來儲存預過濾環境貼圖的資料。為了確保為其 mip 層級分配足夠的記憶體，我們呼叫 glGenerateMipmap，這是一種簡單的方式來分配所需的記憶體量：

unsigned int prefilterMap;
glGenTextures(1, &prefilterMap);
glBindTexture(GL_TEXTURE_CUBE_MAP, prefilterMap);
for (unsigned int i = 0; i < 6; ++i)
{
    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 128, 128, 0, GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

glGenerateMipmap(GL_TEXTURE_CUBE_MAP);

請注意，因為我們打算對 prefilterMap 的 mipmap 進行取樣，所以您需要確保其縮小過濾器（minification filter）設定為 GL_LINEAR_MIPMAP_LINEAR，以啟用三線性過濾（trilinear filtering）。我們將預過濾的鏡面反射結果，儲存在其基礎 mip 層級，每個面的解析度為 128x128。這對於大多數反射來說可能已經足夠，但如果您有大量平滑的材質（例如汽車反射），您可能需要增加解析度。

在上一章節中，我們透過使用球座標，生成均勻分佈在半球 \(\Omega\) 上的取樣向量，來對環境貼圖進行卷積。雖然這對於輻射度來說運作良好，但對於鏡面反射而言效率較低。當談到鏡面反射時，根據表面的粗糙度，光線會緊密或粗略地圍繞著一個法線 \(n\) 上的反射向量 \(r\) 進行反射，但（除非表面極其粗糙）仍然是圍繞著反射向量：

反射光線可能出現的一般形狀被稱為「specular lobe」（鏡面反射波瓣）。隨著粗糙度的增加，鏡面反射波瓣的大小也會增加；而鏡面反射波瓣的形狀會隨著不同的入射光方向而變化。因此，鏡面反射波瓣的形狀高度依賴於材質。

在微表面模型（microsurface model）中，我們可以將鏡面反射波瓣想像成在給定入射光方向下，圍繞著微面半向量（microfacet halfway vectors）的反射方向。由於大多數光線最終都會落在圍繞微面半向量反射的鏡面反射波瓣中，因此以類似的方式產生取樣向量是有意義的，因為否則大多數向量都會被浪費。這個過程被稱為「importance sampling」（重要性取樣）。

蒙地卡羅積分與重要性取樣

要完全掌握重要性取樣，首先了解被稱為「Monte Carlo integration」（蒙地卡羅積分）的數學結構是很有關係的。蒙地卡羅積分主要圍繞著統計學和機率論的結合。蒙地卡羅幫助我們以離散的方式解決一個問題：在不必考慮所有總體的情況下，求出某個總體的某些統計數據或數值。

舉例來說，假設您想計算一個國家所有公民的平均身高。要得到結果，您可以測量每一位公民並計算他們的平均身高，這將給您一個確切的答案。然而，由於大多數國家的人口相當多，這不是一個實際可行的辦法：這會花費太多精力和時間。

另一種方法是挑選一個小得多的完全隨機（無偏）的總體子集，測量他們的身高，並計算結果的平均值。這個子集可以小到只有 100 人。雖然這個答案不像確切答案那樣精準，但您會得到一個相對接近真實答案的結果。這就是所謂的「law of large numbers」（大數法則）。其思想是，如果您從總體中測量一個大小為 \(N\) 的較小、真正隨機的樣本集合，結果將相對接近真實答案，並且隨著樣本數 \(N\) 的增加而越來越接近。

蒙地卡羅積分建立在大數法則之上，並採用同樣的方法來解一個積分。與其為所有可能的（理論上無限的）取樣值 \(x\) 來解一個積分，不如簡單地從總體中隨機挑選 \(N\) 個取樣值並求其平均值。隨著 \(N\) 的增加，我們保證會得到一個更接近積分確切答案的結果：

\[ O = \int\limits_{a}^{b} f(x) dx = \frac{1}{N} \sum_{i=0}^{N-1} \frac{f(x)}{pdf(x)} \]

為了求解積分，我們在總體 \(a\) 到 \(b\) 的範圍內，取 \(N\) 個隨機樣本，將它們加總起來，然後除以樣本總數來求平均。這裡的 \(pdf\) 代表「probability density function」（機率密度函數），它告訴我們在整個樣本集合中，特定樣本出現的機率。例如，一個總體的身高 pdf 會長得有點像這樣：

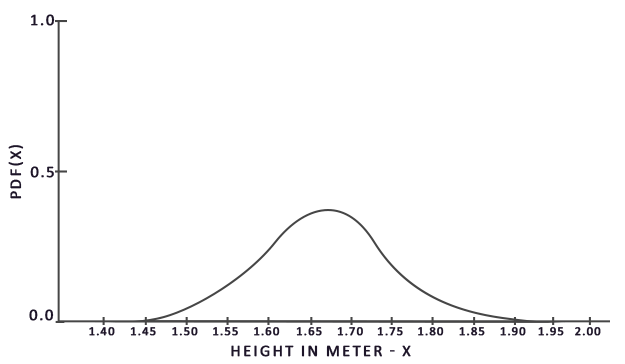
從這張圖我們可以看出，如果我們隨機選取一個總體樣本，選到身高 1.70 公分的人的機率，會比選到身高 1.50 公分的人的機率來得高。

當談到蒙地卡羅積分時，有些樣本被生成的機率可能比其他樣本高。這就是為什麼對於任何一般的蒙地卡羅估計，我們都會根據 pdf 將取樣值除以或乘以樣本機率。到目前為止，在我們估計積分的每個案例中，我們生成的樣本都是均勻的，被生成的機率完全相同。我們到目前為止的估計是「unbiased」（無偏的），這意味著只要樣本數量不斷增加，我們最終會「converge」（收斂）到積分的確切解。

然而，有些蒙地卡羅估計是「biased」（有偏的），這意味著生成的樣本並非完全隨機，而是集中於特定的值或方向。這些有偏的蒙地卡羅估計具有「faster rate of convergence」（更快的收斂速度），這意味著它們可以以更快的速度收斂到確切解，但由於其有偏的性質，它們很可能永遠不會收斂到確切解。這通常是一個可接受的權衡，尤其是在電腦繪圖中，只要結果在視覺上可以接受，確切的解就不是那麼重要。正如我們很快就會在重要性取樣中看到的（它使用了有偏的估計器），生成的樣本偏向於特定的方向，在這種情況下，我們透過將每個樣本乘以或除以其對應的 pdf 來進行彌補。

蒙地卡羅積分在電腦繪圖中相當普遍，因為它是一種相當直觀的方法，可以以離散且高效的方式近似連續積分：選取一個要取樣的區域／體積（例如半球 \(\Omega\)），在該區域／體積內生成 \(N\) 個隨機樣本，並對每個樣本對最終結果的貢獻進行加總和加權。

蒙地卡羅積分是一個廣泛的數學主題，我不會再深入探討細節，但我們會提到有多種方法可以生成「隨機樣本」。預設情況下，每個樣本都是完全（偽）隨機的，就像我們習慣的那樣，但透過利用某些半隨機序列的特性，我們可以生成仍然是隨機的樣本向量，但它們具有有趣的特性。舉例來說，我們可以在一種稱為「low-discrepancy sequences」（低差異序列）的東西上進行蒙地卡羅積分，它仍然會生成隨機樣本，但每個樣本的分佈更均勻（圖片來自 James Heald）：

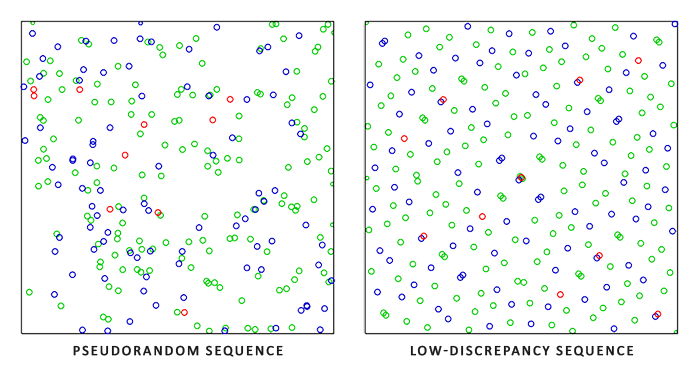
當使用低差異序列來生成蒙地卡羅取樣向量時，這個過程被稱為「Quasi-Monte Carlo integration」（準蒙地卡羅積分）。準蒙地卡羅方法具有更快的「rate of convergence」（收斂速度），這使得它們對於效能密集型應用很有吸引力。

有了我們新學到的蒙地卡羅和準蒙地卡羅積分知識，有一個有趣的特性我們可以利用來獲得更快的收斂速度，那就是「importance sampling」（重要性取樣）。我們在本章節前面已經提過，當談到光的鏡面反射時，反射光向量會被限制在一個鏡面反射波瓣中，其大小由表面的粗糙度決定。由於鏡面反射波瓣之外任何（準）隨機生成的樣本與鏡面反射積分無關，因此將樣本生成集中在鏡面反射波瓣內是有意義的，代價是使蒙地卡羅估計器有偏。

這就是重要性取樣的本質：在由粗糙度限制的某個區域內，圍繞著微面的半向量生成樣本向量。透過將準蒙地卡羅取樣與低差異序列結合，並使用重要性取樣來使樣本向量有偏，我們獲得了高收斂速度。因為我們以更快的速度達到解，我們將需要顯著更少的樣本來達到一個足夠好的近似。

一個低差異序列

在本章節中，我們將使用基於準蒙地卡羅方法的隨機低差異序列，透過重要性取樣來預先計算間接反射方程式的鏡面反射部分。我們將使用的序列是由 [suspicious link removed] 精心描述的「Hammersley Sequence」（漢默斯利序列）。漢默斯利序列基於「Van Der Corput」序列，該序列將十進位二進位表示繞著小數點鏡像。

透過一些巧妙的位元技巧，我們可以非常有效地在 shader 程式中生成 Van Der Corput 序列，我們將用它來獲得在 N 個總樣本中的第 i 個漢默斯利序列樣本：

float RadicalInverse_VdC(uint bits)
{
    bits = (bits << 16u) | (bits >> 16u);
    bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
    bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
    bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
    bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
    return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
    return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}

GLSL 的 Hammersley 函式給了我們在總樣本集大小為 N 中，第 i 個低差異樣本。

不支援位元運算子的漢默斯利序列

並非所有與 OpenGL 相關的驅動程式都支援位元運算子（例如 WebGL 和 OpenGL ES 2.0），在這種情況下，您可能需要使用不依賴位元運算子的 Van Der Corput 序列替代版本：

float VanDerCorput(uint n, uint base)
{
    float invBase = 1.0 / float(base);
    float denom   = 1.0;
    float result  = 0.0;

    for(uint i = 0u; i < 32u; ++i)
    {
        if(n > 0u)
        {
            denom   = mod(float(n), 2.0);
            result += denom * invBase;
            invBase = invBase / 2.0;
            n       = uint(float(n) / 2.0);
        }
    }

    return result;
}
// ----------------------------------------------------------------------------
vec2 HammersleyNoBitOps(uint i, uint N)
{
    return vec2(float(i)/float(N), VanDerCorput(i, 2u));
}

請注意，由於舊硬體中的 GLSL 迴圈限制，該序列會遍歷所有可能的 32 位元。這個版本效能較差，但如果您發現自己沒有位元運算子可用的話，它確實能在所有硬體上運作。

GGX 重要性取樣

我們不再對積分的半球 \(\Omega\) 均勻地或隨機地（蒙地卡羅）生成樣本向量，而是根據表面的粗糙度，生成偏向於微表面半向量（microsurface halfway vector）一般反射方向的樣本向量。取樣過程將與我們之前看到的類似：開始一個大迴圈，生成一個隨機（低差異）序列值，使用這個序列值在切線空間（tangent space）中生成一個樣本向量，將其轉換到世界空間，然後對場景的輻射（radiance）進行取樣。不同之處在於，我們現在使用一個低差異序列值作為輸入來生成一個樣本向量：

const uint SAMPLE_COUNT = 4096u;
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
    vec2 Xi = Hammersley(i, SAMPLE_COUNT);

此外，為了建立樣本向量，我們需要某種方式來定向並使樣本向量偏向於某個表面粗糙度的鏡面反射波瓣。我們可以採用理論章節中描述的 NDF，並按照 Epic Games 的描述，將 GGX NDF 結合到球形樣本向量的過程中：

vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)
{
    float a = roughness*roughness;

    float phi = 2.0 * PI * Xi.x;
    float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
    float sinTheta = sqrt(1.0 - cosTheta*cosTheta);

    // from spherical coordinates to cartesian coordinates
    vec3 H;
    H.x = cos(phi) * sinTheta;
    H.y = sin(phi) * sinTheta;
    H.z = cosTheta;

    // from tangent-space vector to world-space sample vector
    vec3 up        = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
    vec3 tangent   = normalize(cross(up, N));
    vec3 bitangent = cross(N, tangent);

    vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
    return normalize(sampleVec);
}

這根據某些輸入粗糙度和低差異序列值 Xi，給了我們一個大致圍繞著預期微表面半向量定向的樣本向量。請注意，根據 Disney 最初的 PBR 研究，Epic Games 使用粗糙度的平方，以獲得更好的視覺效果。

定義了低差異的漢默斯利序列和樣本生成後，我們就可以完成預過濾卷積 shader 了：

#version 330 core
out vec4 FragColor;
in vec3 localPos;

uniform samplerCube environmentMap;
uniform float roughness;

const float PI = 3.14159265359;

float RadicalInverse_VdC(uint bits);
vec2 Hammersley(uint i, uint N);
vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness);

void main()
{
    vec3 N = normalize(localPos);
    vec3 R = N;
    vec3 V = R;

    const uint SAMPLE_COUNT = 1024u;
    float totalWeight = 0.0;
    vec3 prefilteredColor = vec3(0.0);
    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
    {
        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
        vec3 L  = normalize(2.0 * dot(V, H) * H - V);

        float NdotL = max(dot(N, L), 0.0);
        if(NdotL > 0.0)
        {
            prefilteredColor += texture(environmentMap, L).rgb * NdotL;
            totalWeight      += NdotL;
        }
    }
    prefilteredColor = prefilteredColor / totalWeight;

    FragColor = vec4(prefilteredColor, 1.0);
}

我們根據在預過濾立方體貼圖的每個 mipmap 層級上變化的輸入粗糙度（從 0.0 到 1.0），預過濾環境，並將結果儲存在 prefilteredColor 中。最終的 prefilteredColor 會除以總樣本權重，其中對最終結果影響較小的樣本（對於較小的 NdotL）對最終權重的貢獻也較小。

捕捉預過濾 mipmap 層級

剩下的工作就是讓 OpenGL 使用不同的粗糙度值，在多個 mipmap 層級上預過濾環境貼圖。這實際上用 輻射度 章節的原始設定來做相當容易：

prefilterShader.use();
prefilterShader.setInt("environmentMap", 0);
prefilterShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);

glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
unsigned int maxMipLevels = 5;
for (unsigned int mip = 0; mip < maxMipLevels; ++mip)
{
    // reisze framebuffer according to mip-level size.
    unsigned int mipWidth  = 128 * std::pow(0.5, mip);
    unsigned int mipHeight = 128 * std::pow(0.5, mip);
    glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
    glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, mipWidth, mipHeight);
    glViewport(0, 0, mipWidth, mipHeight);

    float roughness = (float)mip / (float)(maxMipLevels - 1);
    prefilterShader.setFloat("roughness", roughness);
    for (unsigned int i = 0; i < 6; ++i)
    {
        prefilterShader.setMat4("view", captureViews[i]);
        glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0,
                               GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, prefilterMap, mip);

        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
        renderCube();
    }
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);

這個過程與輻射度圖卷積類似，但這次我們將 framebuffer 的維度縮放到適當的 mipmap 比例，每個 mip 層級將維度縮小 2 倍。此外，我們在 glFramebufferTexture2D 的最後一個參數中指定我們正在渲染的 mip 層級，並將我們正在預過濾的粗糙度傳遞給預過濾 shader。

這應該會給我們一個適當預過濾的環境貼圖，我們從 mip 層級越高的地方取樣，它就會返回越模糊的反射。如果我們在天空盒 shader 中使用預過濾的環境立方體貼圖，並強制從其第一個 mip 層級以上的位置取樣，像這樣：

vec3 envColor = textureLod(environmentMap, WorldPos, 1.2).rgb;

我們得到的結果確實看起來像是原始環境的一個更模糊的版本：

如果它看起來有點像，那麼您已經成功預過濾 HDR 環境貼圖了。試著玩玩不同的 mipmap 層級，看看預過濾貼圖如何在 mip 層級增加時，從清晰的反射逐漸變為模糊的反射。

預過濾卷積的渲染瑕疵

儘管目前的預過濾貼圖在大多數情況下都運作良好，但您遲早會遇到一些與預過濾卷積直接相關的渲染瑕疵。我將在這裡列出最常見的，包括如何修復它們。

高粗糙度下的立方體貼圖接縫

在粗糙表面上取樣預過濾貼圖，意味著在它較低的 mip 層級上進行取樣。當取樣立方體貼圖時，OpenGL 預設不會在立方體貼圖面之間進行線性內插。由於較低的 mip 層級解析度較低，並且預過濾貼圖與一個大得多的樣本波瓣進行卷積，因此缺乏「立方體貼圖面之間的過濾」會變得相當明顯：

幸運的是，OpenGL 讓我們可以透過啟用 GL_TEXTURE_CUBE_MAP_SEAMLESS 來正確過濾立方體貼圖面：

glEnable(GL_TEXTURE_CUBE_MAP_SEAMLESS);

只需在應用程式啟動時的某個地方啟用此屬性，接縫就會消失。

預過濾卷積中的亮點

由於鏡面反射中存在高頻細節和變化劇烈的照明強度，對鏡面反射進行卷積需要大量的樣本，才能適當處理 HDR 環境反射變化劇烈的性質。我們已經取了大量的樣本，但在某些環境中，對於一些較粗糙的 mip 層級來說可能仍然不夠，在這種情況下，您會開始看到亮區周圍出現點狀圖案：

一個選項是進一步增加樣本數量，但這對所有環境來說都不夠。正如 Chetan Jags 所描述的，我們可以透過（在預過濾卷積期間）不直接取樣環境貼圖，而是根據積分的 PDF 和粗糙度取樣環境貼圖的一個 mip 層級來減少這種瑕疵：

float D   = DistributionGGX(NdotH, roughness);
float pdf = (D * NdotH / (4.0 * HdotV)) + 0.0001;

float resolution = 512.0; // resolution of source cubemap (per face)
float saTexel  = 4.0 * PI / (6.0 * resolution * resolution);
float saSample = 1.0 / (float(SAMPLE_COUNT) * pdf + 0.0001);

float mipLevel = roughness == 0.0 ? 0.0 : 0.5 * log2(saSample / saTexel);

別忘了在您要從中取樣 mip 層級的環境貼圖上啟用三線性過濾：

glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);

並讓 OpenGL 在立方體貼圖的基礎紋理設定之後生成 mipmap：

// convert HDR equirectangular environment map to cubemap equivalent
[...]
// then generate mipmaps
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
glGenerateMipmap(GL_TEXTURE_CUBE_MAP);

這方法出奇地有效，應該可以移除您預過濾貼圖在較粗糙表面上的大多數，甚至所有的點。

預計算 BRDF

有了正常運作的預過濾環境後，我們可以專注於分離求和近似的第二部分：BRDF。讓我們再次簡要回顧一下鏡面反射的分離求和近似：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} L_i(p,\omega_i) d\omega_i * \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i \]

我們已經在預過濾貼圖中，針對不同的粗糙度等級，預計算了分離求和近似的左半部。右半部則需要我們針對角度 \(n \cdot \omega_o\)、表面粗糙度和菲涅爾的 \(F_0\) 對 BRDF 方程式進行卷積。這類似於用一個純白的環境或常數輻射 \(L_i\) 為 1.0 來整合鏡面反射 BRDF。針對 3 個變數進行 BRDF 卷積有點多，但我們可以試著將 \(F_0\) 從鏡面反射 BRDF 方程式中移出來：

\[ \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) n \cdot \omega_i d\omega_i = \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) \frac{F(\omega_o, h)}{F(\omega_o, h)} n \cdot \omega_i d\omega_i \]

其中 \(F\) 是菲涅爾方程式。將菲涅爾的分母移到 BRDF 中，我們得到以下等效方程式：

\[ \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} F(\omega_o, h) n \cdot \omega_i d\omega_i \]

用菲涅爾-史利克（Fresnel-Schlick）近似來替換最右邊的 \(F\)，我們得到：

\[ \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + (1 - F_0){(1 - \omega_o \cdot h)}^5) n \cdot \omega_i d\omega_i \]

讓我們用 \(\alpha\) 來替換 \({(1 - \omega_o \cdot h)}^5\)，以使其更容易求解 \(F_0\) ：

\[ \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + (1 - F_0)\alpha) n \cdot \omega_i d\omega_i \] \[ \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 + 1*\alpha - F_0*\alpha) n \cdot \omega_i d\omega_i \] \[ \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 * (1 - \alpha) + \alpha) n \cdot \omega_i d\omega_i \]

然後我們將菲涅爾函數 \(F\) 拆分為兩個積分：

\[ \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (F_0 * (1 - \alpha)) n \cdot \omega_i d\omega_i + \int\limits_{\Omega} \frac{f_r(p, \omega_i, \omega_o)}{F(\omega_o, h)} (\alpha) n \cdot \omega_i d\omega_i \]

這樣一來，\(F_0\) 在積分中就是常數，我們可以將 \(F_0\) 移出積分。接著，我們將 \(\alpha\) 替換回其原始形式，得到最終的分離求和 BRDF 方程式：

\[ F_0 \int\limits_{\Omega} f_r(p, \omega_i, \omega_o)(1 - {(1 - \omega_o \cdot h)}^5) n \cdot \omega_i d\omega_i + \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) {(1 - \omega_o \cdot h)}^5 n \cdot \omega_i d\omega_i \]

由此產生的兩個積分分別代表了對 \(F_0\) 的縮放和偏移。請注意，由於 \(f_r(p, \omega_i, \omega_o)\) 中已經包含了一個 \(F\) 的項，所以它們會相互抵消，從 \(f_r\) 中去除了 \(F\) 。

與先前的卷積環境貼圖類似，我們可以在 BRDF 方程式的輸入上進行卷積：\(n\) 和 \(\omega_o\) 之間的角度，以及粗糙度。我們將卷積結果儲存在一個名為「BRDF integration」圖的二維查詢貼圖（LUT）中，我們之後會在 PBR 光照 shader 中使用它，來獲得最終的卷積間接鏡面反射結果。

BRDF 卷積 shader 在一個二維平面上運作，直接使用其二維紋理座標作為 BRDF 卷積的輸入（NdotV 和 roughness）。卷積程式碼與預過濾卷積大致相似，不同之處在於它現在根據我們 BRDF 的幾何函數和菲涅爾-史利克近似來處理樣本向量：

vec2 IntegrateBRDF(float NdotV, float roughness)
{
    vec3 V;
    V.x = sqrt(1.0 - NdotV*NdotV);
    V.y = 0.0;
    V.z = NdotV;

    float A = 0.0;
    float B = 0.0;

    vec3 N = vec3(0.0, 0.0, 1.0);

    const uint SAMPLE_COUNT = 1024u;
    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
    {
        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
        vec3 L  = normalize(2.0 * dot(V, H) * H - V);

        float NdotL = max(L.z, 0.0);
        float NdotH = max(H.z, 0.0);
        float VdotH = max(dot(V, H), 0.0);

        if(NdotL > 0.0)
        {
            float G = GeometrySmith(N, V, L, roughness);
            float G_Vis = (G * VdotH) / (NdotH * NdotV);
            float Fc = pow(1.0 - VdotH, 5.0);

            A += (1.0 - Fc) * G_Vis;
            B += Fc * G_Vis;
        }
    }
    A /= float(SAMPLE_COUNT);
    B /= float(SAMPLE_COUNT);
    return vec2(A, B);
}
// ----------------------------------------------------------------------------
void main()
{
    vec2 integratedBRDF = IntegrateBRDF(TexCoords.x, TexCoords.y);
    FragColor = integratedBRDF;
}

如您所見，BRDF 卷積是數學公式直接轉換為程式碼。我們同時將角度 \(\theta\) 和粗糙度作為輸入，透過重要性取樣生成一個樣本向量，根據 BRDF 的幾何函數和推導出的菲涅爾項對其進行處理，並為每個樣本輸出 \(F_0\) 的縮放和偏移值，最後對它們求平均。

您可能還記得理論章節中提到，BRDF 的幾何項在與 IBL 一起使用時略有不同，因為它的 \(k\) 變數有著稍微不同的解釋：

\[ k_{direct} = \frac{(\alpha + 1)^2}{8} \] \[ k_{IBL} = \frac{\alpha^2}{2} \]

由於 BRDF 卷積是鏡面反射 IBL 積分的一部分，我們將為 Schlick-GGX 幾何函數使用 \(k_{IBL}\)：

float GeometrySchlickGGX(float NdotV, float roughness)
{
    float a = roughness;
    float k = (a * a) / 2.0;

    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}
// ----------------------------------------------------------------------------
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2 = GeometrySchlickGGX(NdotV, roughness);
    float ggx1 = GeometrySchlickGGX(NdotL, roughness);

    return ggx1 * ggx2;
}

請注意，儘管 \(k\) 將 a 作為其參數，但我們並未像最初對 a 的其他解釋那樣，將 roughness 平方後作為 a；很可能是因為 a 在這裡已經被平方了。我不確定這是否是 Epic Games 或最初的 Disney 論文中的不一致之處，但將 roughness 直接轉換為 a 所產生的 BRDF 整合圖與 Epic Games 的版本完全相同。

最後，為了儲存 BRDF 卷積結果，我們將生成一個解析度為 512x512 的二維紋理：

unsigned int brdfLUTTexture;
glGenTextures(1, &brdfLUTTexture);

// pre-allocate enough memory for the LUT texture.
glBindTexture(GL_TEXTURE_2D, brdfLUTTexture);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RG16F, 512, 512, 0, GL_RG, GL_FLOAT, 0);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

請注意，我們使用了 Epic Games 推薦的 16 位元浮點精度格式。務必將包裝模式（wrapping mode）設定為 GL_CLAMP_TO_EDGE 以防止邊緣取樣的瑕疵。

然後，我們重複使用相同的 framebuffer 物件，並在一個 NDC 螢幕空間四邊形上執行這個 shader：

glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, brdfLUTTexture, 0);

glViewport(0, 0, 512, 512);
brdfShader.use();
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
RenderQuad();

glBindFramebuffer(GL_FRAMEBUFFER, 0);

分離求和積分中，卷積後的 BRDF 部分應該會給您以下結果：

有了預過濾環境貼圖和 BRDF 二維 LUT，我們就可以根據分離求和近似來重新建構間接鏡面反射積分。結合後的結果，然後將作為間接或環境鏡面光照。

完成 IBL 反射

為了讓反射方程式的間接鏡面反射部分運作起來，我們需要將分離求和近似的兩部分縫合在一起。讓我們從將預計算的光照數據添加到 PBR shader 的頂部開始：

uniform samplerCube prefilterMap;
uniform sampler2D   brdfLUT;

首先，我們透過使用反射向量取樣預過濾環境貼圖，來獲得表面的間接鏡面反射。請注意，我們根據表面粗糙度取樣適當的 mip 層級，這會讓較粗糙的表面有更模糊的鏡面反射：

void main()
{
    [...]
    vec3 R = reflect(-V, N);

    const float MAX_REFLECTION_LOD = 4.0;
    vec3 prefilteredColor = textureLod(prefilterMap, R,  roughness * MAX_REFLECTION_LOD).rgb;
    [...]
}

在預過濾步驟中，我們只對環境貼圖進行了卷積，最多卷積到 5 個 mip 層級（0 到 4），我們在這裡將其標記為 MAX_REFLECTION_LOD，以確保我們不會取樣到沒有（相關）數據的 mip 層級。

然後，根據材質的粗糙度以及法線和視向量之間夾角，我們從 BRDF 查詢紋理中進行取樣：

vec3 F        = FresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);
vec2 envBRDF  = texture(brdfLUT, vec2(max(dot(N, V), 0.0), roughness)).rg;
vec3 specular = prefilteredColor * (F * envBRDF.x + envBRDF.y);

透過 BRDF 查詢紋理中給予 \(F_0\) 的縮放和偏移（在這裡我們直接使用間接菲涅爾結果 F），我們將其與 IBL 反射方程式的左半部預過濾部分結合，並將近似的積分結果重建為 specular。

這給了我們反射方程式的間接鏡面反射部分。現在，將這部分與上個章節中反射方程式的漫射 IBL 部分結合，我們就得到了完整的 PBR IBL 結果：

vec3 F = FresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness);

vec3 kS = F;
vec3 kD = 1.0 - kS;
kD *= 1.0 - metallic;

vec3 irradiance = texture(irradianceMap, N).rgb;
vec3 diffuse    = irradiance * albedo;

const float MAX_REFLECTION_LOD = 4.0;
vec3 prefilteredColor = textureLod(prefilterMap, R,  roughness * MAX_REFLECTION_LOD).rgb;
vec2 envBRDF  = texture(brdfLUT, vec2(max(dot(N, V), 0.0), roughness)).rg;
vec3 specular = prefilteredColor * (F * envBRDF.x + envBRDF.y);

vec3 ambient = (kD * diffuse + specular) * ao;

請注意，我們沒有將 specular 乘以 kS，因為裡面已經有一個菲涅爾乘法了。

現在，在 PBR 渲染器中，對一系列粗糙度和金屬特性不同的球體執行這段程式碼，我們終於可以看到它們真實的顏色了：

我們甚至可以放飛自我，使用一些很酷的紋理 PBR 材質：

或者載入 Andrew Maximov 製作的這個超棒的免費 3D PBR 模型：

我相信我們都會同意，現在我們的光照看起來更具說服力了。更棒的是，無論我們使用哪種環境貼圖，我們的光照看起來都符合物理學原理。您將在下面看到幾張不同的預計算 HDR 貼圖，它們完全改變了光照動態，但看起來仍然符合物理學原理，而且我們甚至沒有改變任何一個光照變數！

好的，這次的 PBR 冒險之旅可謂相當漫長。由於步驟很多，可能出錯的地方也很多，因此如果您遇到困難，請仔細閱讀 sphere scene 或 textured scene 的程式碼範例（包括所有 shader），或是在評論區檢查並提問。

接下來呢？

希望在本教學結束時，您能對 PBR 有相當清晰的理解，甚至已經有一個實際運作的 PBR 渲染器了。在這些教學中，我們在應用程式啟動時，也就是渲染迴圈之前，預計算了所有相關的 PBR 圖像光照資料。這對於教學目的是很好的，但對於 PBR 的任何實際應用來說就不太理想了。首先，預計算實際上只需要進行一次，而不是每次啟動時都做。其次，當您使用多個環境貼圖時，每次啟動都必須對每一個都進行預計算，這會累積很多時間。

因此，通常的做法是只將環境貼圖預計算成輻射度圖和預過濾圖一次，然後將其儲存到磁碟上（請注意，BRDF 整合圖不依賴於環境貼圖，因此您只需計算或載入它一次）。這意味著您需要設計一個自訂的圖像格式來儲存 HDR 立方體貼圖，包括它們的 mip 層級。或者，您可以將其儲存（和載入）為現有格式之一（例如支援儲存 mip 層級的 .dds）。

此外，我們在這些教學中描述了整個過程，包括生成預計算的 IBL 圖像，以幫助我們進一步理解 PBR 管線。但是，您也可以使用一些很棒的工具，像是 cmftStudio 或 IBLBaker 來為您生成這些預計算的貼圖。

我們略過的一個重點是將預計算的立方體貼圖作為「reflection probes」（反射探測器）：立方體貼圖內插和視差校正（parallax correction）。這個過程是在您的場景中放置幾個反射探測器，在特定位置拍攝場景的立方體貼圖快照，然後我們可以將其卷積成該場景部分的 IBL 資料。透過根據攝影機的遠近，在這些探測器之間進行內插，我們可以實現局部高細節的圖像光照，其限制僅在於我們願意放置多少反射探測器。這樣一來，當從場景中明亮的室外部分移動到較暗的室內部分時，圖像光照就可以正確地更新。我會在未來的某個時候寫一篇關於反射探測器的教學，但現在我推薦下面 Chetan Jags 的文章，它會給您一個好的開始。

延伸閱讀