第三十三章

高級光照 • 點光源陰影

發布時間：2025-07-02 閱讀時間：38 分鐘

在上一章中，我們學會了使用陰影貼圖（shadow mapping）來產生動態陰影。這種方法效果很好，但主要適用於方向光（directional light）或聚光燈（spot light），因為陰影只會沿著光源的方向生成。因此，這種技術也被稱為「方向性陰影貼圖（directional shadow mapping）」，因為深度圖（或稱陰影圖）僅是從光源所看的方向生成的。

本章的重點則是如何在所有方向上產生動態陰影。這項技術非常適合用於點光源（point light），因為真實世界中的點光源會向所有方向投射陰影。這種技術被稱為點光源陰影（point shadows），更正式一點的名稱是「全向陰影貼圖（omnidirectional shadow maps）」。

本章是建立在前一章 陰影貼圖 的基礎之上，因此若您尚未熟悉傳統的陰影貼圖技術，建議先閱讀該章節。

這項技術與方向性陰影貼圖基本上非常類似：我們從光源的視角生成一個深度圖，然後根據當前像素（fragment）的位置來取樣該深度圖，並將每個像素與儲存的深度值進行比較，以判斷該像素是否處於陰影之中。主要的不同點在於所使用的深度圖類型不同。

我們需要的深度圖必須從點光源的所有方向來渲染整個場景，因此普通的 2D 深度圖並不適用。那如果我們改用立方體貼圖（cubemap） 呢？由於立方體貼圖能夠以 6 個面來儲存完整的環境資訊，我們可以將整個場景分別渲染到立方體貼圖的每一個面上，並將這些面作為點光源四周的深度資訊來取樣。

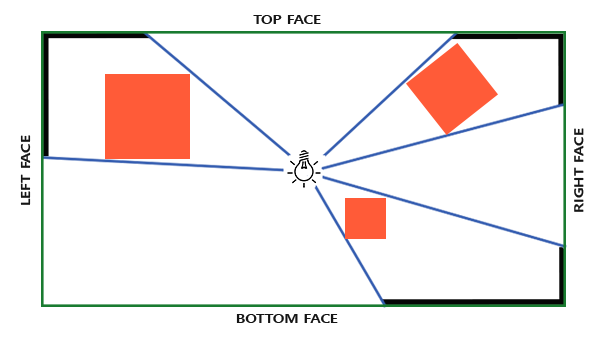
生成的深度立方體貼圖隨後會被傳入光照的 fragment shader中。Shader 會利用一個方向向量來對該 cubemap 進行取樣，以獲得從光源角度看來該片元（fragment）距離最近的深度值。大部分複雜的概念我們已經在上一章的陰影貼圖中討論過了，而這裡困難的部分主要是在於如何生成這個深度 cubemap。

生成深度立方體貼圖（depth cubemap）

為了建立一個光源周圍深度值的 cubemap，我們必須將場景渲染 6 次 —— 每個面一次。其中一個（相當明顯的）方法是：使用 6 個不同的 view 矩陣渲染場景，並每次將 framebuffer 綁定到不同的立方體貼圖面。它的邏輯看起來大概會像這樣：

for(unsigned int i = 0; i < 6; i++)
{
    GLenum face = GL_TEXTURE_CUBE_MAP_POSITIVE_X + i;
    glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, face, depthCubemap, 0);
    BindViewMatrix(lightViewMatrices[i]);
    RenderScene();
}

不過，這種做法的代價相當高，因為僅僅為了生成一張深度圖，就需要進行多次的渲染呼叫（render calls）。在本章中，我們將使用另一種更有組織的替代方法 —— 利用一個幾何著色器（geometry shader）中的小技巧，讓我們只需一次渲染傳遞（single render pass）就能建立整張深度立方體貼圖（depth cubemap）。

首先，我們需要建立一個立方體貼圖（cubemap）：

unsigned int depthCubemap;
glGenTextures(1, &depthCubemap);

並為立方體貼圖中的每一個面（face）分別指定一張具有深度值的 2D 紋理圖像（texture image）：

const unsigned int SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
for (unsigned int i = 0; i < 6; ++i)
        glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_DEPTH_COMPONENT,
                     SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL);

別忘了還要設定這些紋理的參數（texture parameters）：

glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);

一般情況下，我們會將立方體貼圖中的單一面附加到幀緩衝物件（framebuffer object, FBO），然後將場景渲染 6 次，每次都將 framebuffer 的深度緩衝目標切換到不同的立方體貼圖面。

但由於我們接下來會使用幾何著色器（geometry shader），它能讓我們在一次渲染傳遞中對所有面同時進行渲染，因此可以直接使用 glFramebufferTexture 將整個立方體貼圖作為 framebuffer 的 深度附件（depth attachment）來綁定。

glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glFramebufferTexture(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, depthCubemap, 0);
glDrawBuffer(GL_NONE);
glReadBuffer(GL_NONE);
glBindFramebuffer(GL_FRAMEBUFFER, 0);

再次提醒，注意對 glDrawBuffer 和 glReadBuffer 的呼叫：在生成深度立方體貼圖時，我們只關心深度值，因此我們必須明確告訴 OpenGL，這個幀緩衝物件不渲染到顏色緩衝。

對於全向陰影貼圖，我們有兩個渲染階段：首先，我們生成深度立方體貼圖；其次，我們在常規渲染階段中使用深度立方體貼圖，為場景添加陰影。這個過程看起來有點像這樣：

// 1. first render to depth cubemap
glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
    glClear(GL_DEPTH_BUFFER_BIT);
    ConfigureShaderAndMatrices();
    RenderScene();
glBindFramebuffer(GL_FRAMEBUFFER, 0);
// 2. then render scene as normal with shadow mapping (using depth cubemap)
glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
ConfigureShaderAndMatrices();
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
RenderScene();

這個過程與預設的陰影貼圖完全相同，只是這次我們渲染並使用立方體貼圖深度紋理，而不是 2D 深度紋理。

光源空間變換

設定好幀緩衝和立方體貼圖後，我們需要一種方法將場景的所有幾何體轉換到光源在所有 6 個方向上相關的光源空間。就像陰影貼圖章節一樣，我們需要一個光源空間變換矩陣 \(T\)，但這次是每個面一個。

每個光源空間變換矩陣都包含一個投影矩陣和一個視圖矩陣。對於投影矩陣，我們將使用透視投影矩陣；光源代表空間中的一個點，因此透視投影是最合理的。每個光源空間變換矩陣都使用相同的投影矩陣：

float aspect = (float)SHADOW_WIDTH/(float)SHADOW_HEIGHT;
float near = 1.0f;
float far = 25.0f;
glm::mat4 shadowProj = glm::perspective(glm::radians(90.0f), aspect, near, far);

這裡重要的是 glm::perspective 的視野（field of view）參數，我們將其設定為 90 度。透過將其設定為 90 度，我們確保視野足夠大，恰好填滿立方體貼圖的單個面，這樣所有面在邊緣處都能正確對齊。

由於投影矩陣不隨方向改變，我們可以對所有 6 個變換矩陣重複使用它。但是，我們確實需要每個方向不同的視圖矩陣。使用 glm::lookAt，我們創建 6 個視圖方向，每個方向都按照右、左、上、下、近、遠的順序看向立方體貼圖的一個面方向。

std::vector<glm::mat4> shadowTransforms;
shadowTransforms.push_back(shadowProj *
                 glm::lookAt(lightPos, lightPos + glm::vec3( 1.0, 0.0, 0.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj *
                 glm::lookAt(lightPos, lightPos + glm::vec3(-1.0, 0.0, 0.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj *
                 glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 1.0, 0.0), glm::vec3(0.0, 0.0, 1.0));
shadowTransforms.push_back(shadowProj *
                 glm::lookAt(lightPos, lightPos + glm::vec3( 0.0,-1.0, 0.0), glm::vec3(0.0, 0.0,-1.0));
shadowTransforms.push_back(shadowProj *
                 glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 0.0, 1.0), glm::vec3(0.0,-1.0, 0.0));
shadowTransforms.push_back(shadowProj *
                 glm::lookAt(lightPos, lightPos + glm::vec3( 0.0, 0.0,-1.0), glm::vec3(0.0,-1.0, 0.0));

我們在這裡創建了 6 個視圖矩陣，並將它們與投影矩陣相乘，以獲得總共 6 個不同的光源空間變換矩陣。 glm::lookAt 的 target 參數分別指向立方體貼圖的單個面方向。

這些變換矩陣會被發送到負責將深度渲染到立方體貼圖的著色器。

深度著色器

為了將深度值渲染到深度立方體貼圖，我們總共需要三個著色器：一個頂點著色器、一個片段著色器，以及一個介於兩者之間的幾何著色器。

幾何著色器將負責將所有世界空間頂點轉換到 6 個不同的光源空間。因此，頂點著色器只是簡單地將頂點轉換到世界空間並將它們導向幾何著色器：

#version 330 core
layout (location = 0) in vec3 aPos;

uniform mat4 model;

void main()
{
    gl_Position = model * vec4(aPos, 1.0);
}

幾何著色器將輸入 3 個三角形頂點和一個光源空間變換矩陣的 uniform 陣列。幾何著色器負責將頂點轉換到光源空間；這也是它變得有趣的地方。

幾何著色器有一個內建變數 gl_Layer，它指定要將圖元發射到哪個立方體貼圖面。如果保持不變，幾何著色器會像往常一樣將其圖元發送到管線的後續階段，但是當我們更新此變數時，我們可以控制每個圖元要渲染到哪個立方體貼圖面。當然，這只有在我們將立方體貼圖紋理附加到活動幀緩衝時才有效。

#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices=18) out;

uniform mat4 shadowMatrices[6];

out vec4 FragPos; // FragPos from GS (output per emitvertex)

void main()
{
    for(int face = 0; face < 6; ++face)
    {
        gl_Layer = face; // built-in variable that specifies to which face we render.
        for(int i = 0; i < 3; ++i) // for each triangle vertex
        {
            FragPos = gl_in[i].gl_Position;
            gl_Position = shadowMatrices[face] * FragPos;
            EmitVertex();
        }
        EndPrimitive();
    }
}

這個幾何著色器相對簡單。我們輸入一個三角形，並輸出總共 6 個三角形（6 * 3 等於 18 個頂點）。在 main 函式中，我們迭代 6 個立方體貼圖面，透過將面整數儲存到 gl_Layer 中，我們將每個面指定為輸出面。然後，我們透過將每個世界空間輸入頂點與該面的光源空間變換矩陣相乘，將 FragPos 轉換到相關的光源空間，從而生成輸出三角形。請注意，我們還將結果 FragPos 變數發送到片段著色器，我們將需要它來計算深度值。

在上一章中，我們使用了空的片段著色器，讓 OpenGL 自己計算深度貼圖的深度值。這次我們要自己計算（線性）深度，作為每個最近片段位置和光源位置之間的線性距離。計算自己的深度值會讓後續的陰影計算更加直觀。

#version 330 core
in vec4 FragPos;

uniform vec3 lightPos;
uniform float far_plane;

void main()
{
    // get distance between fragment and light source
    float lightDistance = length(FragPos.xyz - lightPos);

    // map to [0;1] range by dividing by far_plane
    lightDistance = lightDistance / far_plane;

    // write this as modified depth
    gl_FragDepth = lightDistance;
}

片段著色器接收來自幾何著色器的 FragPos、光源的位置向量以及視錐體的遠平面值作為輸入。在這裡，我們計算片段與光源之間的距離，將其映射到 [0,1] 範圍，並將其寫入作為片段的深度值。

使用這些著色器和已連接立方體貼圖的幀緩衝物件來渲染場景，應該會為第二次渲染的陰影計算提供一個完全填充的深度立方體貼圖。

全向陰影貼圖

一切設定就緒後，是時候渲染實際的全向陰影了。這個過程與方向性陰影貼圖的章節類似，儘管這次我們綁定的是立方體貼圖紋理而不是 2D 紋理，並且也將光源投影的遠平面變數傳遞給著色器。

glViewport(0, 0, SCR_WIDTH, SCR_HEIGHT);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
shader.use();
// ... send uniforms to shader (including light's far_plane value)
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
// ... bind other textures
RenderScene();

這裡的 renderScene 函式在一個大型立方體房間中渲染了幾個立方體，這些立方體散佈在場景中心的光源周圍。

頂點著色器和片段著色器與原始的陰影貼圖著色器大部分相似：不同之處在於片段著色器不再需要光源空間中的片段位置，因為我們現在可以使用方向向量採樣深度值。

正因為如此，頂點著色器不再需要將其位置向量轉換到光源空間，因此我們可以移除 FragPosLightSpace 變數：

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;

out vec2 TexCoords;

out VS_OUT {
    vec3 FragPos;
    vec3 Normal;
    vec2 TexCoords;
} vs_out;

uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;

void main()
{
    vs_out.FragPos = vec3(model * vec4(aPos, 1.0));
    vs_out.Normal = transpose(inverse(mat3(model))) * aNormal;
    vs_out.TexCoords = aTexCoords;
    gl_Position = projection * view * model * vec4(aPos, 1.0);
}

片段著色器的 Blinn-Phong 光照程式碼與我們之前使用的完全相同，最後加上一個陰影乘法：

#version 330 core
out vec4 FragColor;

in VS_OUT {
    vec3 FragPos;
    vec3 Normal;
    vec2 TexCoords;
} fs_in;

uniform sampler2D diffuseTexture;
uniform samplerCube depthMap;

uniform vec3 lightPos;
uniform vec3 viewPos;

uniform float far_plane;

float ShadowCalculation(vec3 fragPos)
{
    [...]
}

void main()
{
    vec3 color = texture(diffuseTexture, fs_in.TexCoords).rgb;
    vec3 normal = normalize(fs_in.Normal);
    vec3 lightColor = vec3(0.3);
    // ambient
    vec3 ambient = 0.3 * color;
    // diffuse
    vec3 lightDir = normalize(lightPos - fs_in.FragPos);
    float diff = max(dot(lightDir, normal), 0.0);
    vec3 diffuse = diff * lightColor;
    // specular
    vec3 viewDir = normalize(viewPos - fs_in.FragPos);
    vec3 reflectDir = reflect(-lightDir, normal);
    float spec = 0.0;
    vec3 halfwayDir = normalize(lightDir + viewDir);
    spec = pow(max(dot(normal, halfwayDir), 0.0), 64.0);
    vec3 specular = spec * lightColor;
    // calculate shadow
    float shadow = ShadowCalculation(fs_in.FragPos);
    vec3 lighting = (ambient + (1.0 - shadow) * (diffuse + specular)) * color;

    FragColor = vec4(lighting, 1.0);
}

這裡有一些細微的差異：光照程式碼是相同的，但我們現在有一個 samplerCube uniform，而且 ShadowCalculation 函式以當前片段的位置作為其參數，而不是光源空間中的片段位置。我們現在也包含了光源視錐體的 far_plane 值，我們稍後會用到它。

最大的差異在於 ShadowCalculation 函式的內容，它現在從立方體貼圖而不是 2D 紋理採樣深度值。讓我們一步一步地討論其內容。

我們首先要做的是檢索立方體貼圖的深度。您可能還記得本章的立方體貼圖部分，我們將深度儲存為片段與光源位置之間的線性距離；我們在這裡採用類似的方法：

float ShadowCalculation(vec3 fragPos)
{
    vec3 fragToLight = fragPos - lightPos;
    float closestDepth = texture(depthMap, fragToLight).r;
}

這裡我們取得片段位置和光源位置之間的差向量，並將該向量作為方向向量來採樣立方體貼圖。方向向量不需要是單位向量即可從立方體貼圖中採樣，因此無需對其進行正規化。結果 closestDepth 值是光源與其最近可見片段之間經過正規化的深度值。

closestDepth 值目前在 [0,1] 讀值範圍內，因此我們首先將其乘以 far_plane，使它轉換回 [0,far_plane] 範圍。

closestDepth *= far_plane;

接下來，我們取得當前片段與光源之間的深度值，由於我們在立方體貼圖中計算深度值的方式，我們可以透過 fragToLight 的長度輕鬆獲得這個值：

float currentDepth = length(fragToLight);

這會回傳一個與 closestDepth 相同（或更大）範圍的深度值。

現在我們可以比較這兩個深度值，看看哪個離光源更近，並判斷當前片段是否處於陰影中。我們也包含了陰影偏移（shadow bias），這樣就不會像上一章討論的那樣出現陰影痤瘡（shadow acne）。

float bias = 0.05;
float shadow = currentDepth -  bias > closestDepth ? 1.0 : 0.0;

完整的 ShadowCalculation 函式就會變成這樣：

float ShadowCalculation(vec3 fragPos)
{
    // get vector between fragment position and light position
    vec3 fragToLight = fragPos - lightPos;
    // use the light to fragment vector to sample from the depth map
    float closestDepth = texture(depthMap, fragToLight).r;
    // it is currently in linear range between [0,1]. Re-transform back to original value
    closestDepth *= far_plane;
    // now get current linear depth as the length between the fragment and light position
    float currentDepth = length(fragToLight);
    // now test for shadows
    float bias = 0.05;
    float shadow = currentDepth -  bias > closestDepth ? 1.0 : 0.0;

    return shadow;
}

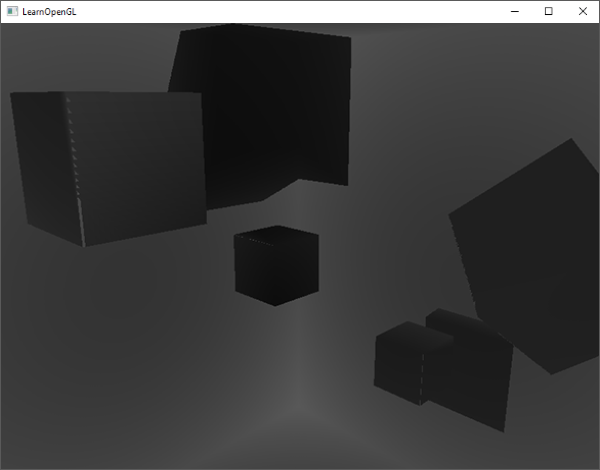
有了這些著色器，我們就能得到相當不錯的陰影，而且這次是點光源在所有方向上的陰影。當點光源位於簡單場景的中心時，看起來會有點像這樣：

你可以在這裡找到這個範例的原始碼。

視覺化立方體貼圖深度緩衝

如果你跟我有點像，可能第一次嘗試時並未能正確實現，所以進行一些偵錯是有道理的。其中一個明顯的檢查就是驗證深度貼圖是否正確建立。一個簡單的技巧是，取出 ShadowCalculation 函式中的 closestDepth 變數，並將該變數顯示為：

FragColor = vec4(vec3(closestDepth / far_plane), 1.0);

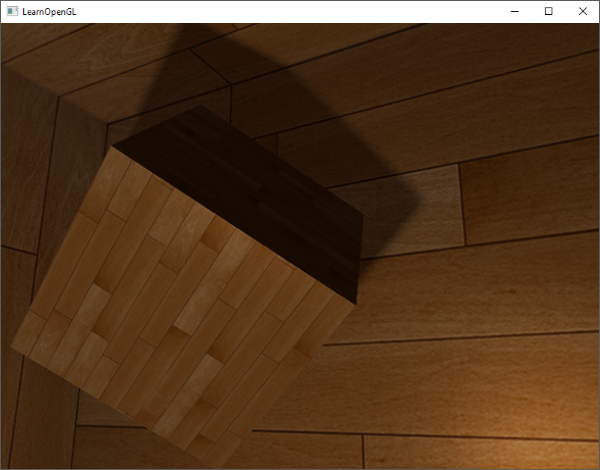
結果會是一個灰階的場景，其中每個顏色代表場景的線性深度值：

你也可以看到外牆上即將被陰影籠罩的區域。如果看起來有些相似，你就知道深度立方體貼圖已經正確生成了。

PCF

由於全向陰影貼圖基於傳統陰影貼圖的相同原理，因此它也具有相同的解析度相關瑕疵。如果你放大得足夠近，你將再次看到鋸齒狀邊緣。近距離百分比篩選（Percentage-closer filtering，簡稱 PCF）允許我們透過在片段位置周圍篩選多個樣本並平均結果來平滑這些鋸齒狀邊緣。

如果我們採用上一章相同的簡單 PCF 濾波器並添加第三個維度，我們將得到：

float shadow  = 0.0;
float bias    = 0.05;
float samples = 4.0;
float offset  = 0.1;
for(float x = -offset; x < offset; x += offset / (samples * 0.5))
{
    for(float y = -offset; y < offset; y += offset / (samples * 0.5))
    {
        for(float z = -offset; z < offset; z += offset / (samples * 0.5))
        {
            float closestDepth = texture(depthMap, fragToLight + vec3(x, y, z)).r;
            closestDepth *= far_plane;   // undo mapping [0;1]
            if(currentDepth - bias > closestDepth)
                shadow += 1.0;
        }
    }
}
shadow /= (samples * samples * samples);

程式碼與傳統的陰影貼圖程式碼並沒有太大不同。我們根據固定數量的樣本，動態計算並添加每個軸的紋理偏移。對於每個樣本，我們在偏移後的採樣方向上重複原始的陰影處理過程，並在最後將結果平均。

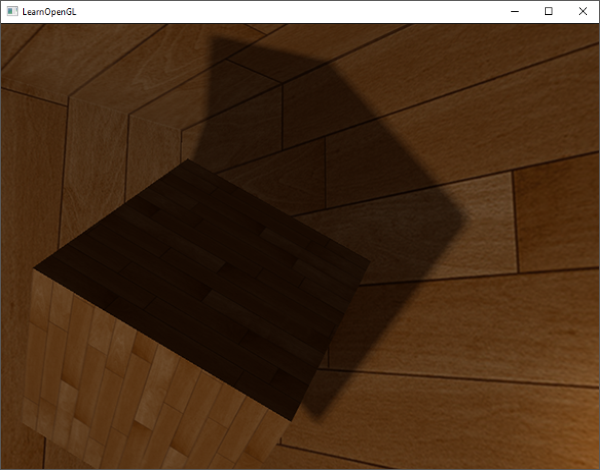
現在的陰影看起來更柔和、更平滑，並呈現出更合理的結果。

然而，當 samples 設定為 4.0 時，我們每個片段總共會取樣 64 次，這可真是不少！

由於這些取樣大多是多餘的，因為它們都在原始方向向量附近取樣，所以只在垂直於取樣方向向量的方向上取樣可能更有意義。然而，由於沒有（簡單的）方法可以找出哪些子方向是多餘的，這就變得困難了。我們可以使用的一個技巧是，採用一個偏移方向的陣列，這些方向都大致可分離，例如，每個方向都指向完全不同的方向。這將顯著減少彼此接近的子方向數量。下面就是這樣一個最多 20 個偏移方向的陣列：

vec3 sampleOffsetDirections[20] = vec3[]
(
   vec3( 1,  1,  1), vec3( 1, -1,  1), vec3(-1, -1,  1), vec3(-1,  1,  1),
   vec3( 1,  1, -1), vec3( 1, -1, -1), vec3(-1, -1, -1), vec3(-1,  1, -1),
   vec3( 1,  1,  0), vec3( 1, -1,  0), vec3(-1, -1,  0), vec3(-1,  1,  0),
   vec3( 1,  0,  1), vec3(-1,  0,  1), vec3( 1,  0, -1), vec3(-1,  0, -1),
   vec3( 0,  1,  1), vec3( 0, -1,  1), vec3( 0, -1, -1), vec3( 0,  1, -1)
);

從這裡我們可以調整 PCF 演算法，從 sampleOffsetDirections 中取得固定數量的樣本，並用這些樣本來採樣立方體貼圖。這樣做的好處是，我們需要更少的樣本就能獲得視覺上相似的結果。

float shadow = 0.0;
float bias   = 0.15;
int samples  = 20;
float viewDistance = length(viewPos - fragPos);
float diskRadius = 0.05;
for(int i = 0; i < samples; ++i)
{
    float closestDepth = texture(depthMap, fragToLight + sampleOffsetDirections[i] * diskRadius).r;
    closestDepth *= far_plane;   // undo mapping [0;1]
    if(currentDepth - bias > closestDepth)
        shadow += 1.0;
}
shadow /= float(samples);

這裡我們在原始的 fragToLight 方向向量周圍，添加了多個由 diskRadius 縮放的偏移量，以便從立方體貼圖中取樣。

另一個我們可以應用的有趣技巧是，我們可以根據觀察者到片段的距離來改變 diskRadius，使得陰影在遠處更柔和，而在近處更銳利。

float diskRadius = (1.0 + (viewDistance / far_plane)) / 25.0;

更新後的 PCF 演算法產生了同樣好，甚至更好的柔和陰影效果：

當然，我們添加到每個樣本的 bias（偏差）高度依賴於上下文，並且總是需要根據您正在處理的場景進行調整。請嘗試調整所有這些數值，看看它們如何影響場景。

您可以在這裡找到最終的程式碼：這裡。

我應該提一下，使用幾何著色器生成深度貼圖，不一定會比為每個面渲染場景 6 次來得快。像這樣使用幾何著色器有其自身的效能損耗，這可能會抵消最初使用它所帶來的效能提升。這當然取決於環境類型、特定的顯示卡驅動程式以及許多其他因素。因此，如果你真的想從系統中榨取最大效能，請務必對這兩種方法進行分析，並為你的場景選擇更有效率的那一個。

額外資源