第四十一章

PBR • 光照

發布時間：2025-08-04 閱讀時間：29 分鐘

在上一章中，我們為一個逼真的物理基礎渲染器奠定了基礎。在本章中，我們將專注於將先前討論的理論轉化為一個實際的渲染器，該渲染器使用直接（或解析）光源：例如點光源（point lights）、定向光源（directional lights）和/或聚光燈（spotlights）。

讓我們從回顧上一章的最終反射方程開始：

\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]

我們現在大致了解發生了什麼，但仍然是一個巨大的未知數是，我們究竟要如何表示輻照度（irradiance），也就是場景的總輻射（total radiance）\(L\)。我們知道，輻射（radiance）\(L\)（在電腦圖學領域的解釋）是測量給定立體角 \(\omega\) 上光源的輻射通量（radiant flux）\(\phi\) 或光能。在我們的案例中，我們假設立體角 \(\omega\) 是無限小的，在這種情況下，輻射測量的是光源在單一光線或方向向量上的通量。

有了這些知識，我們該如何將其轉化為我們從先前章節中累積的一些光照知識呢？好吧，想像我們有一個點光源（point light source，一個在所有方向上都發出相同亮度的光源），其輻射通量轉換為 RGB 三元組為 (23.47, 21.31, 20.79)。這個光源的輻射強度（radiant intensity）等於它在所有出射方向上的輻射通量。然而，當我們對表面上的一個特定點 \(p\) 進行著色時，在其半球 \(\Omega\) 上所有可能的入射光方向中，只有一個入射方向向量 \(w_i\) 是直接來自點光源的。因為我們的場景中只有一個光源，並且假設它是一個空間中的單點，所以在表面點 \(p\) 上觀察到的所有其他可能的入射光方向的輻射都為零：

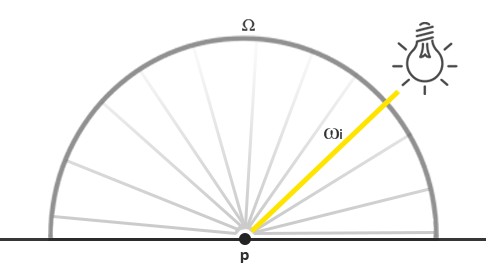
如果我們一開始假設光線衰減（光線隨距離變暗）不影響點光源，那麼無論我們將光源放置在哪裡，入射光線的輻射都是相同的（不包括用入射角 \(\cos \theta\) 對輻射進行縮放）。這是因為點光源的輻射強度與我們觀察它的角度無關，有效地將其輻射強度模擬為其輻射通量：一個常數向量 (23.47, 21.31, 20.79)。

然而，輻射也將位置 \(p\) 作為輸入，並且由於任何逼真的點光源都會考慮光線衰減，因此點光源的輻射強度會根據點 \(p\) 和光源之間距離的一些測量值進行縮放。然後，根據從原始輻射方程中提取的內容，結果會根據表面法線 \(n\) 和入射光方向 \(w_i\) 之間的點積進行縮放。

用更實際的術語來說：在直接點光源的情況下，輻射函數 \(L\) 測量的是光的顏色，根據其與 \(p\) 的距離進行衰減，並根據 \(n \cdot w_i\) 進行縮放，但僅限於撞擊 \(p\) 的單一光線 \(w_i\)，該光線等於從 \(p\) 到光源的方向向量。在程式碼中，這轉化為：

vec3  lightColor  = vec3(23.47, 21.31, 20.79);
vec3  wi          = normalize(lightPos - fragPos);
float cosTheta    = max(dot(N, Wi), 0.0);
float attenuation = calculateAttenuation(fragPos, lightPos);
vec3  radiance    = lightColor * attenuation * cosTheta;

除了術語不同之外，這段程式碼對您來說應該非常熟悉：這正是我們到目前為止一直在做的漫射照明。對於直接照明，輻射的計算方式與我們之前計算照明的方式類似，因為只有一個光線方向向量會影響表面的輻射。

請注意，這個假設成立是因為點光源是無限小且僅為空間中的單個點。如果我們要模擬一個具有面積或體積的光源，它的輻射在多個入射光方向上將是非零的。

對於源自單個點的其他類型光源，我們也以類似的方式計算輻射。例如，定向光源具有恆定的 \(w_i\) 而沒有衰減因子。而聚光燈的輻射強度則不是恆定的，而是會根據聚光燈的前向方向向量進行縮放。

這也讓我們回到表面半球 \(\Omega\) 上的積分 \(\int\)。由於我們在著色單個表面點時，事先知道所有貢獻光源的單一位置，因此不需要嘗試求解積分。我們可以直接取得（已知）光源的數量，並計算它們的總輻照度，前提是每個光源只有一個光線方向會影響表面的輻射。這使得在直接光源上的 PBR 相對簡單，因為我們實際上只需要遍歷貢獻光源即可。當我們稍後在 IBL 章節中考慮環境光照時，我們確實必須考慮積分，因為光線可以來自任何方向。

一個 PBR 表面模型

讓我們從編寫一個實作上述 PBR 模型的片段著色器開始。首先，我們需要取得對表面著色所必需的 PBR 相關輸入：

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;

uniform vec3 camPos;

uniform vec3  albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;

我們使用從通用頂點著色器計算出的標準輸入，以及物件表面的一組恆定材質屬性。

然後在片段著色器的一開始，我們進行任何照明演算法所需的常見計算：

void main()
{
    vec3 N = normalize(Normal);
    vec3 V = normalize(camPos - WorldPos);
    [...]
}

直接光照

在本章的範例演示中，我們總共有 4 個點光源，它們共同代表了場景的輻照度。為了滿足反射方程，我們遍歷每個光源，計算其各自的輻射，並將其貢獻（由 BRDF 和光的入射角縮放）相加。我們可以將這個迴圈視為針對直接光源求解 \(\Omega\) 上的積分 \(\int\)。首先，我們計算每個光源的相關變數：

vec3 Lo = vec3(0.0);
for(int i = 0; i < 4; ++i)
{
    vec3 L = normalize(lightPositions[i] - WorldPos);
    vec3 H = normalize(V + L);

    float distance    = length(lightPositions[i] - WorldPos);
    float attenuation = 1.0 / (distance * distance);
    vec3 radiance     = lightColors[i] * attenuation;
    [...]

由於我們在線性空間中計算光照（我們會在著色器末尾進行 gamma 校正），我們使用更符合物理的「平方反比定律」來衰減光源。

雖然這符合物理，但您可能仍然希望使用 constant-linear-quadratic 衰減方程，它（雖然不符合物理）可以讓您對光的能量衰減有更多控制。

然後，對於每個光源，我們需要計算完整的 Cook-Torrance 高光 BRDF 項：

\[ \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)} \]

我們想做的第一件事是計算高光反射和漫射反射之間的比例，或者說表面反射光線的比例與折射光線的比例。我們從上一章知道，Fresnel 方程正好計算了這個值（請注意這裡的 clamp 是為了防止出現黑點）：

vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
    return F0 + (1.0 - F0) * pow(clamp(1.0 - cosTheta, 0.0, 1.0), 5.0);
}

Fresnel-Schlick 近似需要一個 F0 參數，它被稱為零入射下的表面反射率，或者說如果直接看著表面時，表面會反射多少光。F0 因材質而異，並且在金屬上會被染色，就像我們在大型材質資料庫中發現的那樣。在 PBR 金屬工作流程中，我們做了一個簡化的假設：大多數電介質表面在 F0 為 0.04 的情況下看起來是視覺上正確的，而我們則將金屬表面的 F0 指定為反照率值。這轉化為程式碼如下：

vec3 F0 = vec3(0.04);
F0      = mix(F0, albedo, metallic);
vec3 F  = fresnelSchlick(max(dot(H, V), 0.0), F0);

如您所見，對於非金屬表面，F0 始終為 0.04。對於金屬表面，我們根據 metallic 屬性在原始 F0 和反照率值之間進行線性插值來改變 F0。

有了 \(F\) 之後，剩下的需要計算的項是法線分佈函數 \(D\) 和幾何函數 \(G\)。

在一個直接 PBR 光照著色器中，它們對應的程式碼是：

float DistributionGGX(vec3 N, vec3 H, float roughness)
{
    float a      = roughness*roughness;
    float a2     = a*a;
    float NdotH  = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;

    float num   = a2;
    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
    denom = PI * denom * denom;

    return num / denom;
}

float GeometrySchlickGGX(float NdotV, float roughness)
{
    float r = (roughness + 1.0);
    float k = (r*r) / 8.0;

    float num   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return num / denom;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2  = GeometrySchlickGGX(NdotV, roughness);
    float ggx1  = GeometrySchlickGGX(NdotL, roughness);

    return ggx1 * ggx2;
}

這裡需要注意的是，與理論章節相反，我們將粗糙度（roughness）參數直接傳遞給這些函數；透過這種方式，我們可以對原始粗糙度值進行一些特定於項目的修改。根據 Disney 的觀察並被 Epic Games 採納，在幾何（geometry）和法線分佈（normal distribution）函數中將粗糙度平方，光照看起來會更正確。

定義了這兩個函數後，在反射迴圈中計算 NDF 和 G 項就變得簡單了：

float NDF = DistributionGGX(N, H, roughness);
float G   = GeometrySmith(N, V, L, roughness);

這讓我們有足夠的資訊來計算 Cook-Torrance BRDF：

vec3 numerator    = NDF * G * F;
float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0)  + 0.0001;
vec3 specular     = numerator / denominator;

請注意，我們在分母中加上了 0.0001，以防止在任何點積結果為 0.0 時發生除以零的錯誤。

現在我們終於可以計算每個光源對反射方程的貢獻了。由於 Fresnel 值直接對應於 \(k_S\)，我們可以使用 F 來表示任何擊中表面的光的鏡面反射貢獻。然後，我們可以從 \(k_S\) 計算折射的比例 \(k_D\)：

vec3 kS = F;
vec3 kD = vec3(1.0) - kS;

kD *= 1.0 - metallic;

考慮到 kS 代表被反射的光能，剩餘的光能比例就是被折射的光，我們將其儲存為 kD。此外，因為金屬表面不折射光，因此也沒有漫反射，我們透過在表面是金屬時將 kD 歸零來強制執行此屬性。這為我們提供了計算每個光源的出射反射值所需的最終資料：

const float PI = 3.14159265359;

    float NdotL = max(dot(N, L), 0.0);
    Lo += (kD * albedo / PI + specular) * radiance * NdotL;
}

得到的 Lo 值，也就是出射輻射（outgoing radiance），實際上是反射方程在 \(\Omega\) 上的積分 \(\int\) 的結果。我們不需要試圖求解所有可能入射光方向的積分，因為我們確切地知道有 4 個入射光方向會影響這個片段（fragment）。因此，我們可以直接遍歷這些入射光方向，也就是場景中的光源數量。

剩下的就是給直接照明結果 Lo 添加一個（臨時的）環境光項，然後我們就得到了片段的最終光照顏色：

vec3 ambient = vec3(0.03) * albedo * ao;
vec3 color   = ambient + Lo;

線性與 HDR 渲染

到目前為止，我們假設所有的計算都在線性色彩空間中進行，為此我們需要在著色器的末尾進行 gamma 校正。在線性空間中計算光照至關重要，因為 PBR 要求所有輸入都是線性的。不考慮這一點將導致不正確的光照結果。此外，我們希望光照輸入接近其物理等效值，這樣它們的輻射或顏色值可以在高光譜範圍內劇烈變化。結果，Lo 的值可能會迅速變得非常高，然後因為預設的低動態範圍（LDR）輸出而被限制在 0.0 和 1.0 之間。我們透過在 gamma 校正之前，對 Lo 進行色調或曝光映射，將 高動態範圍（HDR）值正確地對應到 LDR 來解決這個問題：

color = color / (color + vec3(1.0));
color = pow(color, vec3(1.0/2.2));

在這裡，我們使用 Reinhard 運算子對 HDR 顏色進行色調映射，保留了可能高度變化的輻照度所帶來的高動態範圍，然後我們對顏色進行 gamma 校正。我們沒有獨立的幀緩衝區或後處理階段，所以我們可以直接在前向片段著色器的末尾同時應用色調映射和 gamma 校正步驟。

在 PBR 管線中，考慮線性色彩空間和高動態範圍至關重要。如果沒有這些，就不可能正確地捕捉不同光強度的細節，您的計算會出錯，導致視覺上不討喜。

完整的直接光照 PBR 著色器

現在剩下的就是將最終經過色調映射和 gamma 校正的顏色傳遞到片段著色器的輸出通道，我們就有了一個直接 PBR 光照著色器。為了完整起見，完整的 main 函數如下：

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;

// material parameters
uniform vec3  albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;

// lights
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];

uniform vec3 camPos;

const float PI = 3.14159265359;

float DistributionGGX(vec3 N, vec3 H, float roughness);
float GeometrySchlickGGX(float NdotV, float roughness);
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness);
vec3 fresnelSchlick(float cosTheta, vec3 F0);

void main()
{
    vec3 N = normalize(Normal);
    vec3 V = normalize(camPos - WorldPos);

    vec3 F0 = vec3(0.04);
    F0 = mix(F0, albedo, metallic);

    // reflectance equation
    vec3 Lo = vec3(0.0);
    for(int i = 0; i < 4; ++i)
    {
        // calculate per-light radiance
        vec3 L = normalize(lightPositions[i] - WorldPos);
        vec3 H = normalize(V + L);
        float distance    = length(lightPositions[i] - WorldPos);
        float attenuation = 1.0 / (distance * distance);
        vec3 radiance     = lightColors[i] * attenuation;

        // cook-torrance brdf
        float NDF = DistributionGGX(N, H, roughness);
        float G   = GeometrySmith(N, V, L, roughness);
        vec3 F    = fresnelSchlick(max(dot(H, V), 0.0), F0);

        vec3 kS = F;
        vec3 kD = vec3(1.0) - kS;
        kD *= 1.0 - metallic;

        vec3 numerator    = NDF * G * F;
        float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.0001;
        vec3 specular     = numerator / denominator;

        // add to outgoing radiance Lo
        float NdotL = max(dot(N, L), 0.0);
        Lo += (kD * albedo / PI + specular) * radiance * NdotL;
    }

    vec3 ambient = vec3(0.03) * albedo * ao;
    vec3 color = ambient + Lo;

    color = color / (color + vec3(1.0));
    color = pow(color, vec3(1.0/2.2));

    FragColor = vec4(color, 1.0);
}

希望藉由上一章的理論和反射方程的知識，這個著色器不再那麼令人畏懼。如果我們拿這個著色器、4 個點光源，以及相當多的球體，並在它們的垂直和水平軸上分別改變它們的金屬度和粗糙度值，我們會得到類似以下的結果：

從下到上，金屬度（metallic）值從 0.0 到 1.0，粗糙度（roughness）從左到右從 0.0 增加到 1.0。您可以看到，僅僅透過改變這兩個簡單易懂的參數，我們就可以展示各種不同的材質。

您可以在這裡找到這個範例的完整原始碼。

紋理化 PBR (Textured PBR)

將系統擴展為現在可以將其表面參數作為紋理（textures）而不是 uniform 值來接收，這使我們能夠針對每個片段（per-fragment）來控制表面材質的屬性：

[...]
uniform sampler2D albedoMap;
uniform sampler2D normalMap;
uniform sampler2D metallicMap;
uniform sampler2D roughnessMap;
uniform sampler2D aoMap;

void main()
{
    vec3 albedo     = pow(texture(albedoMap, TexCoords).rgb, 2.2);
    vec3 normal     = getNormalFromNormalMap();
    float metallic  = texture(metallicMap, TexCoords).r;
    float roughness = texture(roughnessMap, TexCoords).r;
    float ao        = texture(aoMap, TexCoords).r;
    [...]
}

請注意，藝術家提供的反照率紋理（albedo textures）通常是在 sRGB 空間中製作的，這就是為什麼我們在使用反照率進行光照計算之前，先將它們轉換為線性空間。根據藝術家用於生成環境遮蔽貼圖（ambient occlusion maps）的系統，您可能也需要將它們從 sRGB 轉換為線性空間。而金屬度和粗糙度貼圖幾乎總是在線性空間中製作。

用紋理替換上一組球體的材質屬性，已經顯示出比我們之前使用的光照演算法有顯著的視覺提升：

您可以在這裡找到帶有紋理的範例完整原始碼，並在這裡找到使用的紋理集（帶有一個白色的 ao 貼圖）。請記住，金屬表面在直接光照環境中往往看起來太暗，因為它們沒有漫反射。當考慮環境的鏡面反射環境光照（specular ambient lighting）時，它們看起來會更正確，這正是我們在接下來的章節中將重點關注的內容。

儘管我們還沒有內建基於影像的光照（image based lighting），因此我們的渲染器不像您在網路上找到的一些 PBR 渲染範例那樣令人印象深刻，但我們現在擁有的系統仍然是一個物理基礎的渲染器，即使沒有 IBL，您也會看到您的光照看起來真實很多。