第三十四章

高級光照 • 法線貼圖 (Normal Mapping)

發布時間：2025-07-02 閱讀時間：42 分鐘

我們的場景都塞滿了網格（Mesh），每個網格由數百或數千個三角形組成。我們透過將 2D 紋理包裹在這些平面三角形上，來提高真實感，隱藏了多邊形只是微小平面三角形的事實。紋理確實有幫助，但是當你仔細觀察網格時，仍然很容易看到底層的平面。然而，大多數現實生活中的表面都不是平坦的，並且會呈現出許多（凹凸不平的）細節。

舉例來說，拿磚牆表面來說。磚牆表面是一種相當粗糙的表面，顯然不完全平坦：它包含凹陷的水泥條紋和許多細小的孔洞和裂縫。如果我們在有光照的場景中觀察這樣的磚牆表面，沉浸感很容易被打破。下面我們可以看到應用在平面上，並由點光源照明的磚牆紋理。

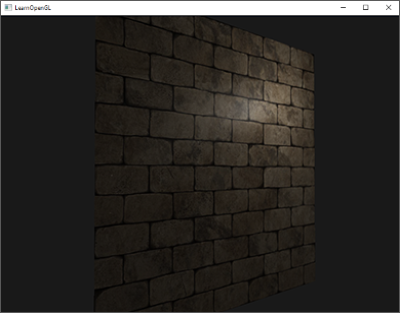
光照沒有考慮到任何小裂縫和孔洞，並且完全忽略了磚塊之間深陷的條紋；表面看起來完美平坦。我們可以部分地透過使用鏡面貼圖（specular map）來修復這種扁平的外觀，假裝某些表面由於深度或其他細節而光照較少，但這更像是一種 HACK 而不是真正的解決方案。我們需要的是一種方法，可以讓光照系統了解表面所有微小的類似深度的細節。

如果我們從光的角度來思考這個問題：為什麼表面會被當作完全平坦的表面來照亮？答案就是表面的法向量。從光照技術的角度來看，它判斷物體形狀的唯一方法是透過其垂直的法向量。磚牆表面只有一個單一的法向量，因此表面會根據該法向量的方向均勻地受光照。如果我們不使用每個片元都相同的「每個表面法向量」，而是使用每個片元都不同的「每個片元法向量」會怎麼樣？這樣我們就可以根據表面的微小細節稍微改變法向量；這會給人一種表面複雜許多的錯覺：

透過使用逐片元法線，我們可以欺騙光照系統，讓它誤以為物體表面由許多微小平面（垂直於法向量）組成，從而大幅提升表面的細節。這種與逐表面法線相比，使用逐片元法線的技術稱為「法線貼圖（normal mapping）」或「凹凸貼圖（bump mapping）」。應用在磚塊平面上，看起來會像這樣：

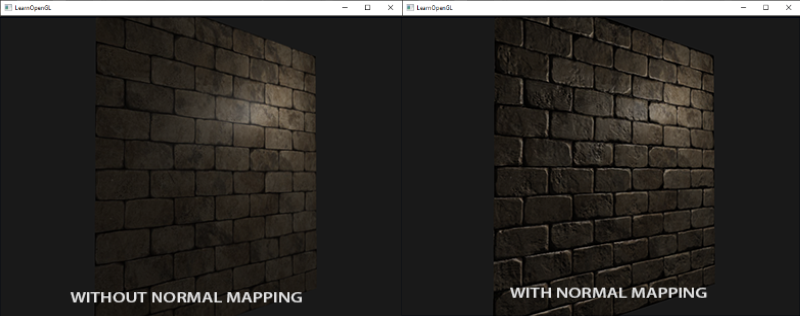
如您所見，這大幅提升了細節，而且成本相對較低。由於我們只改變每個片元的法向量，因此無需更改光照方程式。現在我們將逐片元的法向量（而不是經過插值的表面法向量）傳遞給光照演算法。剩下的就交給光照演算法處理了。

法線貼圖 (Normal Mapping)

為了讓法線貼圖運作，我們需要一個逐片元的法線。類似於我們處理漫射貼圖 (diffuse map) 和鏡面貼圖 (specular map) 的方式，我們可以使用 2D 紋理來儲存逐片元的法線資料。這樣一來，我們就可以透過取樣 2D 紋理來取得該特定片元的法向量。

儘管法向量是幾何實體，而紋理通常只用於顏色資訊，但將法向量儲存在紋理中可能不會立即顯而易見。如果你想想紋理中的顏色向量，它們是以具有 r、g 和 b 分量的 3D 向量表示的。我們也可以類似地將法向量的 x、y 和 z 分量儲存在各自的顏色分量中。法向量的範圍介於 -1 到 1 之間，因此它們會先被映射到 [0,1]：

vec3 rgb_normal = normal * 0.5 + 0.5; // transforms from [-1,1] to [0,1]

將法向量轉換為像這樣的 RGB 顏色分量後，我們就可以將從表面形狀導出的逐片元法向量儲存到 2D 紋理中。本章開頭磚牆表面的「法線貼圖 (normal map)」範例如下所示：

這張（以及幾乎所有您在網路上找到的法線貼圖）都會帶有藍色的色調。這是因為所有法線都密切指向正 z 軸 $(0, 0, 1)$：一種藍色的顏色。顏色上的偏差代表法線向量略微偏離了一般的正 z 方向，賦予紋理深度感。例如，您可以看到每塊磚塊的頂部顏色趨向於更綠，這是合理的，因為磚塊的頂部法線會更多地指向正 y 方向 $(0, 1, 0)$，這恰好是綠色！

對於一個簡單的平面，當我們看向正 z 軸時，我們可以將這張漫射紋理和這張法線貼圖用於渲染前一節的圖像。請注意，連結的法線貼圖與上面顯示的不同。原因在於 OpenGL 讀取紋理座標的方式與紋理通常的建立方式相反，y (或 v) 座標是反轉的。因此，連結的法線貼圖的 y (或綠色) 分量是反轉的（您可以看到綠色現在指向下方）；如果您未能考慮到這一點，光照將會不正確。載入這兩張紋理，將它們綁定到正確的紋理單元，並在光照片段著色器中進行以下更改來渲染一個平面：

uniform sampler2D normalMap;

void main()
{
    // obtain normal from normal map in range [0,1]
    normal = texture(normalMap, fs_in.TexCoords).rgb;
    // transform normal vector to range [-1,1]
    normal = normalize(normal * 2.0 - 1.0);

    [...]
    // proceed with lighting as normal
}

在這裡，我們將採樣到的法線顏色從 [0,1] 重新映射回 [-1,1]，反轉了法線到 RGB 顏色的映射過程，然後將採樣到的法向量用於後續的光照計算。在這個範例中，我們使用了 Blinn-Phong 著色器。

透過隨時間緩慢移動光源，您將能真正感受到法線貼圖所帶來的深度感。執行此法線貼圖範例會得到與本章開頭所示完全相同的結果：

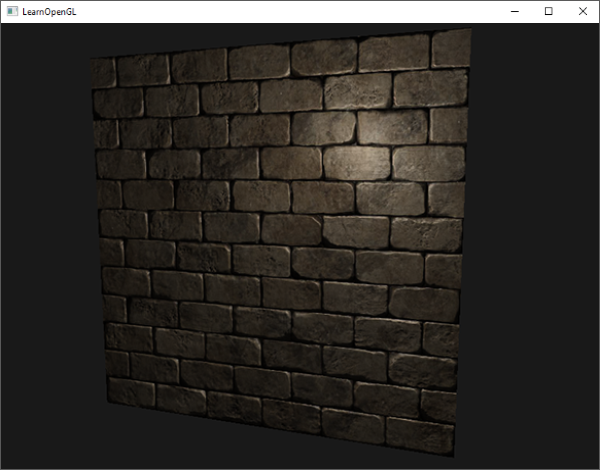
然而，這種法線貼圖的使用方式存在一個很大的限制。我們使用的法線貼圖，其法線向量都或多或少指向正 Z 方向。這是因為平面的表面法線也指向正 Z 方向，所以才能正常運作。但是，如果我們將相同的法線貼圖應用到一個平鋪在地板上、表面法線向量指向正 Y 方向的平面上，會發生什麼事呢？

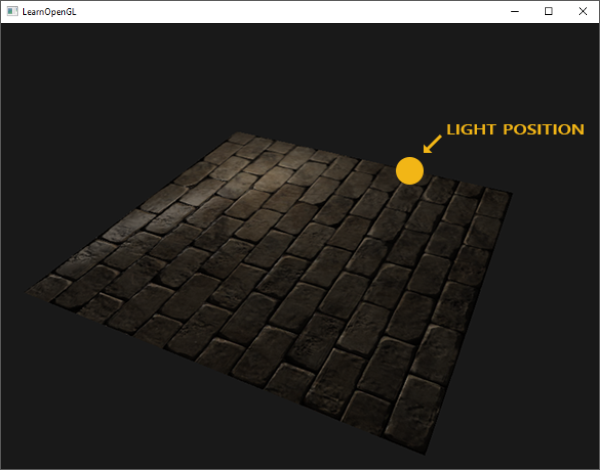
光照看起來不對勁！發生這種情況的原因是，即使這個平面的採樣法線應該主要指向正 y 方向，它們仍然大致指向正 z 方向。結果是，光照系統認為表面的法線與之前平面指向正 z 方向時相同；光照計算是錯誤的。下圖顯示了採樣法線在此表面上大致的樣子：

你可以看到所有法線都或多或少指向正 z 方向，儘管它們應該指向正 y 方向。解決這個問題的一個方法是為表面每個可能的方向定義一個法線貼圖；在立方體的情況下，我們將需要 6 個法線貼圖。然而，對於可能有多達數百種表面方向的高級網格，這將成為一個不可行的方法。

存在另一種解決方案，它在不同的座標空間中執行所有光照計算：在這個座標空間中，法線貼圖向量始終指向正 z 方向；所有其他光照向量都相對於這個正 z 方向進行變換。這樣我們就可以始終使用相同的法線貼圖，無論方向如何。這個座標空間稱為「切線空間 (tangent space)」。

切線空間

法線貼圖中的法線向量是在切線空間中表示的，其中法線始終大致指向正 z 方向。切線空間是三角形表面局部的一個空間：法線相對於個別三角形的局部參考框架。可以將其視為法線貼圖向量的局部空間；無論最終的變換方向如何，它們都被定義為指向正 z 方向。然後，我們可以使用特定的矩陣將法線向量從這個局部切線空間變換到世界或視圖座標，使其沿著最終映射表面的方向定向。

假設我們有上一節中指向正 y 方向的錯誤法線貼圖表面。法線貼圖是在切線空間中定義的，因此解決問題的一種方法是計算一個矩陣，將法線從切線空間變換到另一個空間，使其與表面的法線方向對齊：這樣法線向量都大致指向正 y 方向。切線空間的優點在於我們可以為任何類型的表面計算這個矩陣，以便我們可以正確地將切線空間的 z 方向與表面的法線方向對齊。

這樣的矩陣稱為「TBN」矩陣，其中字母代表「切線 (Tangent)」、「副切線 (Bitangent)」和「法線 (Normal)」向量。這些是我們構建此矩陣所需的向量。為了構建這樣一個基底變換矩陣，它將切線空間向量變換到不同的座標空間，我們需要三個沿著法線貼圖表面對齊的垂直向量：一個向上、向右和向前向量；類似於我們在 攝影機 章節中所做的。

我們已經知道向上向量，它是表面的法線向量。向右和向前向量分別是切線向量和副切線向量。下圖顯示了表面上的所有三個向量：

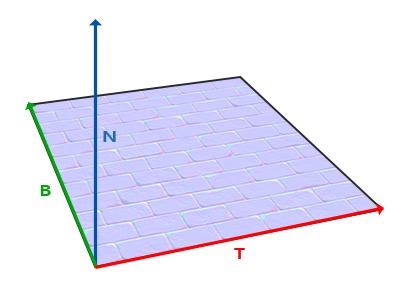
計算切線（tangent）與副切線（bitangent）向量不像法線向量那麼直接。從圖片中可以看出，法線貼圖中切線與副切線的方向，與我們定義表面紋理座標的方向一致。我們將利用這一點，來為每個表面計算其切線與副切線向量。要獲取它們需要一些數學運算，請參考下圖：

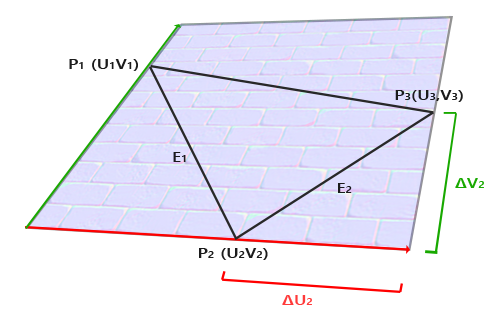
從圖中可以看到，三角形一條邊 \(E_2\) 的紋理座標差（記作 \(\Delta U_2\) 和 \(\Delta V_2\)）與切線向量 \(T\) 和副切線向量 \(B\) 的方向相同。因此，我們可以將圖中所示的兩條邊 \(E_1\) 和 \(E_2\) 表示為切線向量 \(T\) 和副切線向量 \(B\) 的線性組合：

\[E_1 = \Delta U_1T + \Delta V_1B\] \[E_2 = \Delta U_2T + \Delta V_2B\]

我們也可以將其寫成：

\[(E_{1x}, E_{1y}, E_{1z}) = \Delta U_1(T_x, T_y, T_z) + \Delta V_1(B_x, B_y, B_z)\] \[(E_{2x}, E_{2y}, E_{2z}) = \Delta U_2(T_x, T_y, T_z) + \Delta V_2(B_x, B_y, B_z)\]

我們可以將 \(E\) 計算為三角形兩個頂點位置之間的差向量，而 \(\Delta U\) 和 \(\Delta V\) 則是它們的紋理座標差。這樣我們就得到了兩個未知數（切線 \(T\) 和副切線 \(B\)）以及兩個方程式。你或許還記得代數課上教的知識，這使我們能夠解出 \(T\) 和 \(B\)。

最後這個方程式可以用另一種形式表示：矩陣乘法的形式：

\[\begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix} \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} \]

試著在腦海中想像這個矩陣乘法的過程，確認這確實是相同的方程式。將這些方程式改寫為矩陣形式的一個優點是，求解 \(T\) 和 \(B\) 會變得更容易理解。如果我們將兩邊同時乘以 \(\Delta U \Delta V\) 矩陣的反矩陣，就能得到：

\[ \begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{bmatrix}^{-1} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} = \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} \]

這讓我們能夠求出 \(T\) 和 \(B\)。這需要我們計算 delta 紋理座標矩陣的反矩陣。我不會深入說明如何計算矩陣的反矩陣，但大致可以理解為：取該矩陣行列式的倒數，然後乘以它的伴隨矩陣：

\[ \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{bmatrix} = \frac{1}{\Delta U_1 \Delta V_2 - \Delta U_2 \Delta V_1} \begin{bmatrix} \Delta V_2 & -\Delta V_1 \\ -\Delta U_2 & \Delta U_1 \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} \]

這個最終的方程式提供了一種根據三角形的兩條邊和其紋理座標來計算切線向量 \(T\) 和副切線向量 \(B\) 的公式。

如果你不是完全理解其中的數學內容也不用擔心。只要你明白我們可以從三角形的頂點和紋理座標（因為紋理座標與切線向量在同一空間中）來計算切線與副切線向量，那你就已經成功了一半了。

手動計算切線與副切線

在先前的示範中，我們使用了一個朝向正 z 方向的簡單法線貼圖平面。這次我們想要使用切線空間來實作法線貼圖，這樣我們就可以隨意改變這個平面的方向，而法線貼圖依然能正常運作。藉由前面討論過的數學方法，我們將手動計算這個表面的切線與副切線向量。

我們假設這個平面是由以下向量構成的（由 1, 2, 3 和 1, 3, 4 這兩個三角形組成）：

// positions
glm::vec3 pos1(-1.0,  1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
glm::vec3 pos3( 1.0, -1.0, 0.0);
glm::vec3 pos4( 1.0,  1.0, 0.0);
// texture coordinates
glm::vec2 uv1(0.0, 1.0);
glm::vec2 uv2(0.0, 0.0);
glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// normal vector
glm::vec3 nm(0.0, 0.0, 1.0);

我們首先計算第一個三角形的邊與 UV 座標的差值：

glm::vec3 edge1 = pos2 - pos1;
glm::vec3 edge2 = pos3 - pos1;
glm::vec2 deltaUV1 = uv2 - uv1;
glm::vec2 deltaUV2 = uv3 - uv1;

有了計算切線與副切線所需的資料後，我們就可以依照前一節的方程式進行計算：

float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);

tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);

bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);

[...] // 計算平面第二個三角形的切線／副切線時使用相同的方法

這裡我們先將方程中的分數部分預先計算為 f，然後對每個向量分量進行對應的矩陣運算，再乘以 f。如果你將這段程式碼與最終方程式進行比較，就會發現它是一種直接的翻譯。由於三角形總是平面的，我們每個三角形只需計算一組切線／副切線向量即可，因為它們對該三角形的所有頂點而言是相同的。

最後算出的切線與副切線向量應該分別為 (1, 0, 0) 與 (0, 1, 0)，再加上法線 (0, 0, 1)，可以形成一個正交的 TBN 矩陣。將其視覺化在平面上，TBN 向量將會呈現如下：

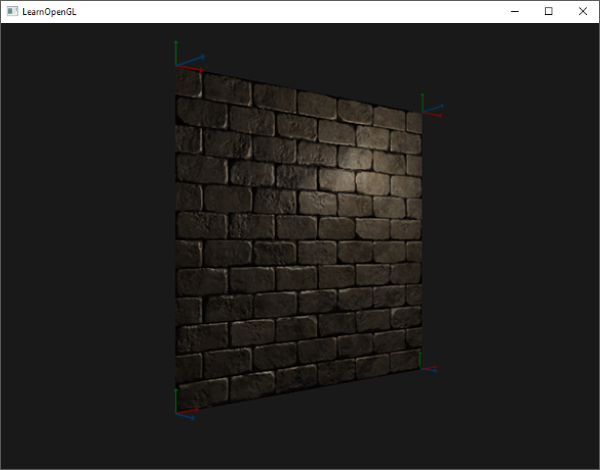
當每個頂點都定義了切線與副切線向量之後，我們就可以開始實作真正的法線貼圖了。

切線空間法線貼圖

為了讓法線貼圖能夠運作，我們首先需要在著色器中建立一個 TBN 矩陣。為了做到這一點，我們需要將先前計算出的切線與副切線向量作為頂點屬性傳遞給頂點著色器：

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in vec3 aTangent;
layout (location = 4) in vec3 aBitangent;

接著在頂點著色器的 main 函式中，我們建立 TBN 矩陣：

void main()
{
   [...]
   vec3 T = normalize(vec3(model * vec4(aTangent,   0.0)));
   vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0)));
   vec3 N = normalize(vec3(model * vec4(aNormal,    0.0)));
   mat3 TBN = mat3(T, B, N);
}

這裡我們首先將所有 TBN 向量轉換到我們想要工作的座標系中，在本例中是世界空間，因為我們將它們與 model 矩陣相乘。然後，我們直接使用 mat3 的建構子，提供對應的列向量來建立實際的 TBN 矩陣。請注意，如果我們想要更加精確，應該使用法線矩陣來乘以 TBN 向量，因為我們只關心向量的方向。

技術上來說，在頂點著色器中其實不需要 bitangent 這個變數。TBN 中的三個向量彼此垂直，所以我們可以在頂點著色器中自行通過 T 和 N 向量的叉積來計算 bitangent：vec3 B = cross(N, T);

那麼現在我們已經有了 TBN 矩陣，我們要如何使用它呢？對於法線貼圖來說，有兩種使用 TBN 矩陣的方法，我們將展示這兩種做法：

  1. 使用 TBN 矩陣將任意向量從切線空間轉換到世界空間，並將該矩陣傳遞到片段著色器中，然後使用它將從法線貼圖中採樣到的法線從切線空間轉換到世界空間，這樣該法線就與其他光照變數處於相同的空間中。
  2. 取 TBN 矩陣的反矩陣，將任意向量從世界空間轉換到切線空間，然後使用這個矩陣不是去轉換法線，而是將其他相關的光照變數轉換到切線空間中；這樣法線仍然與其他光照變數處於相同的空間中。

我們先來看第一種情況。我們從法線貼圖中採樣到的法線向量是以切線空間表示的，而其他光照向量（例如光源方向與視角方向）則是以世界空間表示的。透過將 TBN 矩陣傳遞給片段著色器，我們可以將採樣得到的切線空間法線向量乘上 TBN 矩陣，從而將其轉換為世界空間，這樣它就與其他光照向量處於相同的參考空間中。這樣做，所有的光照計算（尤其是點積運算）才有意義。

將 TBN 矩陣傳遞到片段著色器是很簡單的：

out VS_OUT {
    vec3 FragPos;
    vec2 TexCoords;
    mat3 TBN;
} vs_out;

void main()
{
    [...]
    vs_out.TBN = mat3(T, B, N);
}

在片段著色器中，我們同樣將 mat3 作為輸入變數：

in VS_OUT {
    vec3 FragPos;
    vec2 TexCoords;
    mat3 TBN;
} fs_in;

有了這個 TBN 矩陣，我們現在可以更新法線貼圖的程式碼，加入從切線空間到世界空間的轉換：

normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normal * 2.0 - 1.0;
normal = normalize(fs_in.TBN * normal);

因為計算後的 normal 現在是在世界空間中，所以不需要更動片段著色器中其他程式碼，因為光照計算部分假設法線向量是世界空間的。

接著，我們來看看第二種情況，我們取 TBN 矩陣的反矩陣，將所有相關的世界空間向量轉換到採樣法線所處的空間：切線空間。TBN 矩陣的構造方式不變，但在傳送到片段著色器之前先對矩陣求轉置（即反矩陣）：

vs_out.TBN = transpose(mat3(T, B, N));

注意這裡我們使用的是 transpose 函數而非 inverse 函數。正交矩陣（各軸皆為垂直單位向量）的一個優良特性是：其轉置矩陣等於其反矩陣。這很棒，因為計算反矩陣成本較高，而轉置矩陣計算成本低很多。

在片段著色器中，我們不轉換法線向量，而是將其他相關向量轉換到切線空間，即將 lightDir 和 viewDir 向量轉換。這樣，每個向量都處於相同的座標空間：切線空間。

void main()
{
    vec3 normal = texture(normalMap, fs_in.TexCoords).rgb;
    normal = normalize(normal * 2.0 - 1.0);

    vec3 lightDir = fs_in.TBN * normalize(lightPos - fs_in.FragPos);
    vec3 viewDir  = fs_in.TBN * normalize(viewPos - fs_in.FragPos);
    [...]
}

第二種方法看起來工作量比較大，且需要在片段著色器中進行矩陣乘法，那我們為何還要用第二種方法呢？

原因是，將向量從世界空間轉換到切線空間有一個額外好處：我們可以將所有相關的光照向量提前在頂點著色器中轉換成切線空間，而不用在片段著色器中做。這可行，因為 lightPos 和 viewPos 不會在每個片段執行時更新，而 fs_in.FragPos 的切線空間位置也可以在頂點著色器中計算，並讓片段插值自動完成。換句話說，在片段著色器中幾乎不需要再將向量轉換到切線空間，而在第一種方法中因為採樣的法線向量是針對每個片段執行時獨有的，所以必須轉換。

因此，我們不把 TBN 矩陣的反矩陣傳入片段著色器，而是傳送切線空間的光源位置、視角位置和頂點位置。這樣可節省片段著色器中的矩陣乘法計算。這是個不錯的優化，因為頂點著色器執行次數遠低於片段著色器。這也是為什麼這種做法常被採用的原因。

out VS_OUT {
    vec3 FragPos;
    vec2 TexCoords;
    vec3 TangentLightPos;
    vec3 TangentViewPos;
    vec3 TangentFragPos;
} vs_out;

uniform vec3 lightPos;
uniform vec3 viewPos;

[...]

void main()
{
    [...]
    mat3 TBN = transpose(mat3(T, B, N));
    vs_out.TangentLightPos = TBN * lightPos;
    vs_out.TangentViewPos  = TBN * viewPos;
    vs_out.TangentFragPos  = TBN * vec3(model * vec4(aPos, 1.0));
}

然後在片段著色器中，我們使用這些新的輸入變數在切線空間中計算光照。因為法線向量已經在切線空間中，光照計算才會合理。

使用切線空間法線貼圖後，我們應該會得到與本章開頭相似的結果。但這次，我們可以任意旋轉平面，光照效果仍然正確：

glm::mat4 model = glm::mat4(1.0f);
model = glm::rotate(model, (float)glfwGetTime() * -10.0f, glm::normalize(glm::vec3(1.0, 0.0, 1.0)));
shader.setMat4("model", model);
RenderQuad();

效果確實看起來像是正確的法線貼圖：

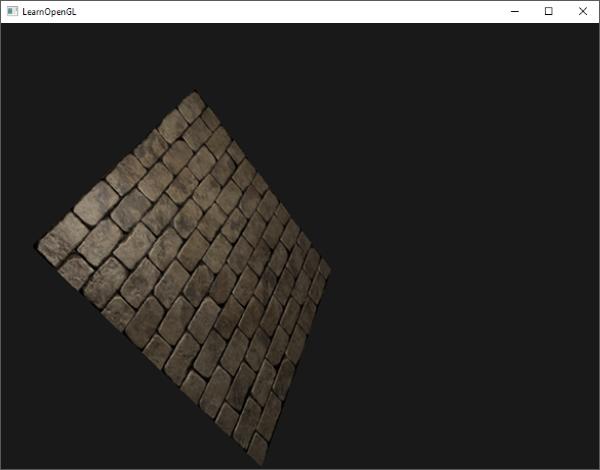
您可以在這裡找到源代碼。

複雜物件

我們已經展示了如何使用法線貼圖以及切線空間變換，透過手動計算切線和副切線向量來實現。幸運的是，我們不需要經常手動計算這些向量。大多數情況下，你只需要在自訂模型加載器中實現一次，或者像我們這裡一樣，使用基於 Assimp 的模型加載器。

Assimp 提供了一個非常實用的配置選項，叫做 aiProcess_CalcTangentSpace，在加載模型時可以啟用它。當你將 aiProcess_CalcTangentSpace 位元傳給 Assimp 的 ReadFile 函式時，Assimp 會為每個載入的頂點計算平滑的切線和副切線向量，類似於我們本章節所做的。

const aiScene *scene = importer.ReadFile(
    path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace
);

在 Assimp 中，我們可以透過以下方式取得計算出的切線：

vector.x = mesh->mTangents[i].x;
vector.y = mesh->mTangents[i].y;
vector.z = mesh->mTangents[i].z;
vertex.Tangent = vector;

接著，你需要更新模型加載器，使其也能從有紋理的模型中載入法線貼圖。Wavefront 物件格式 (.obj) 的法線貼圖匯出方式與 Assimp 的慣例略有不同，因為 aiTextureType_NORMAL 不會載入法線貼圖，而 aiTextureType_HEIGHT 則會：

vector<Texture> normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal");

當然，不同類型的模型及檔案格式情況也不同。

使用更新後的模型加載器，針對帶有鏡面反射與法線貼圖的模型執行應用程式，效果如下：

如你所見，法線貼圖可以以極低的額外成本大幅提升物件細節。

使用法線貼圖也是提升效能的好方法。在使用法線貼圖之前，你需要使用大量頂點來讓網格有高細節。透過法線貼圖，我們能以較少的頂點數達成相同的細節層級。以下這張來自 Paolo Cignoni 的圖片，展示了兩種方法的比較：

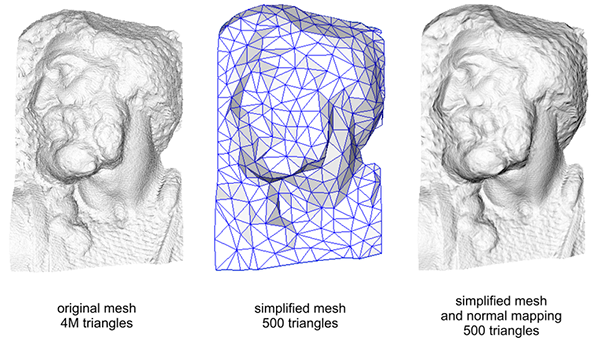
高頂點網格與低頂點網格加上法線貼圖後的細節幾乎無法區分。因此，法線貼圖不僅好看，更是個絕佳工具，可以用較低頂點數的網格替代高頂點數的網格，而不會（或幾乎不會）損失細節。

最後一點

還有一個技巧值得討論，可以稍微提升品質，但不會帶來太大額外成本。

當切線向量在大量共享許多頂點的較大網格上計算時，通常會對切線向量進行平均，以產生平滑的結果。這種作法的問題是三個 TBN 向量可能不再垂直，導致最終的 TBN 矩陣不再是正交矩陣。非正交的 TBN 矩陣會讓法線貼圖結果略有偏差，但我們仍可加以改進。

利用數學上的「Gram-Schmidt 正交化過程」，我們可以「重新正交化」TBN 向量，使得每個向量彼此再次垂直。在頂點著色器中，我們可以這麼做：

vec3 T = normalize(vec3(model * vec4(aTangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0)));
// 以 N 作為參考，重新正交化 T
T = normalize(T - dot(T, N) * N);
// 再透過 T 與 N 的叉積取得垂直的 B 向量
vec3 B = cross(N, T);

mat3 TBN = mat3(T, B, N);

這樣做雖然只是小幅提升，但通常能以較低的成本提升法線貼圖的結果。你也可以觀看額外資源中 Normal Mapping Mathematics 影片的結尾部分，裡面對這個過程有精彩的解說。

額外資源