第十二章

光 • 基本光照

發布時間：2025-06-26 閱讀時間：33 分鐘

譯者總結：本文介紹了 Phong 光照模型！非常基礎，非常容易理解，是一篇極好的解釋圖形領域光照模型存在的現實理由及其實現辦法。Phong 模型裡，物件最終呈現出來的光是三種光的組合：1. 環境光；2. 散光（漫反射）；3. 高光（反射光或者鏡面光）。文章分別對此三者進行的現實意義的解釋以及計算機層面的實現方案。結合最終程序運行，筆者將每一步實現的結果展現給讀者，讓讀者明白筆者說的到底“是什麼”。

現實世界中的光照極為複雜，且取決於太多因素，以我們有限的處理能力無法負擔計算。因此，OpenGL 中的光照是基於對現實的近似，使用簡化的模型，這些模型更容易處理，並且看起來相對相似。這些光照模型基於我們對光的物理學理解。其中一種模型稱為 Phong 光照模型。Phong 光照模型的主要組成部分包含三個分量：環境光（ambient）、漫反射光（diffuse）和鏡面反射光（specular）。你可以在下面看到這些光照分量單獨和組合起來的效果：

  • 環境光照（Ambient lighting）：即使在黑暗中，世界上通常仍然存在一些光線（月亮、遠處的光源），所以物體幾乎從不完全黑暗。為了模擬這一點，我們使用一個環境光照常數，它總是給物體一些顏色。
  • 漫反射光照（Diffuse lighting）：模擬光源對物體的方向性影響。這是光照模型中視覺上最重要的組成部分。物體某個部分越是面向光源，它就變得越亮。
  • 鏡面反射光照（Specular lighting）：模擬出現在閃亮物體上的光線亮點。鏡面高光比物體本身的顏色更傾向於光的顏色。

為了創建視覺上有趣的場景，我們至少要模擬這三個光照分量。我們將從最簡單的一個開始：環境光照。

環境光照（Ambient lighting）

光線通常不是來自單一光源，而是來自我們周圍散佈的許多光源，即使它們不立即 P 可見。光的一個特性是它可以在許多方向上散射和反射，到達不直接可見的地方；因此，光可以反射到其他表面，並對物體的光照產生間接影響。考慮到這一點的演算法稱為全域照明演算法，但這些演算法複雜且計算成本高昂。

由於我們不喜歡複雜且昂貴的演算法，我們將從一個非常簡單的全域照明模型開始，即環境光照。如您在前一節中看到的，我們使用一個小的常數（光）顏色，將其添加到物體片段的最終結果顏色中，從而使其看起來總是有一些散射光，即使沒有直接光源也是如此。

為場景添加環境光照非常簡單。我們取光的顏色，將其乘以一個小的常數環境因子，再將其乘以物體的顏色，然後將其用作立方體物體著色器中片段的顏色：

void main()
{
    float ambientStrength = 0.1;
    vec3 ambient = ambientStrength * lightColor;

    vec3 result = ambient * objectColor;
    FragColor = vec4(result, 1.0);
}

如果您現在執行程式，會注意到光照的第一個階段已成功應用於物體。物體相當暗，但並非完全黑暗，因為環境光照已應用（請注意，光照立方體不受影響，因為我們使用了不同的著色器）。它看起來應該像這樣：

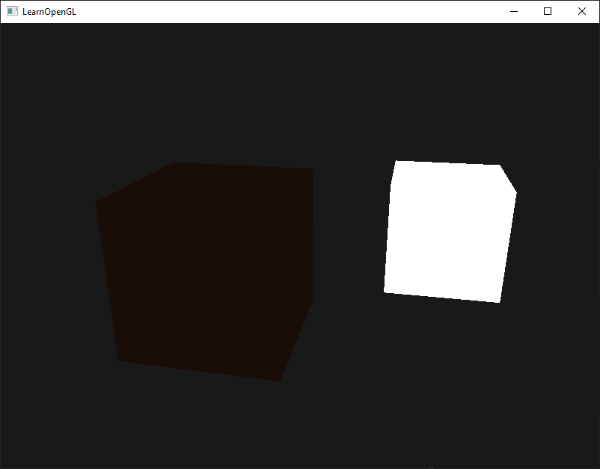
漫反射光照（Diffuse lighting）

單獨的環境光照無法產生最有趣的結果，但漫反射光照將開始對物體產生顯著的視覺影響。漫反射光照會使物體的片段越是與來自光源的光線對齊，其亮度就越高。為了讓您更好地理解漫反射光照，請看下圖：

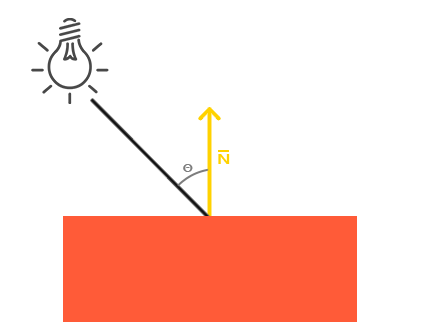
左側是光源，光線射向物體的一個單一片段。我們需要測量光線接觸片段的角度。如果光線垂直於物體表面，則光線的影響最大。為了測量光線與片段之間的角度，我們使用一種稱為法線向量的東西，它是一個垂直於片段表面的向量（此處顯示為黃色箭頭）；我們稍後會講到這一點。然後可以使用點積輕鬆計算兩個向量之間的角度。

您可能還記得座標轉換章節中提到，兩個單位向量之間的角度越小，點積就越傾向於值 1。當兩個向量之間的角度為 90 度時，點積變為 0。同樣適用於 $\theta$：$\theta$ 越大，光線對片段顏色的影響就越小。

請注意，為了獲得兩個向量之間角度的（僅）餘弦值，我們將使用單位向量（長度為 1 的向量），因此我們需要確保所有向量都已正規化，否則點積返回的不僅僅是餘弦值（參見座標轉換）。

因此，點積的結果返回一個標量，我們可以用它來計算光線對片段顏色的影響，從而根據片段相對於光線的方向產生不同亮度的片段。

那麼，我們需要計算漫反射光照的內容：

  • 法線向量：垂直於頂點表面的向量。
  • 定向光線：一個方向向量，它是光源位置和片段位置之間的差向量。為了計算這條光線，我們需要光源的位置向量和片段的位置向量。

法向量（Normal vectors）

法線向量是垂直於頂點表面的（單位）向量。由於頂點本身沒有表面（它只是空間中的一個點），我們透過使用其周圍的頂點來確定頂點的表面，從而獲取法線向量。我們可以使用一個小技巧，透過叉積來計算所有立方體頂點的法線向量，但由於 3D 立方體不是複雜的形狀，我們可以簡單地手動將它們添加到頂點資料中。更新後的頂點資料陣列可以在這裡找到。請試著想像法線確實是垂直於每個平面表面的向量（立方體由 6 個平面組成）。

由於我們向頂點陣列添加了額外的資料，我們應該更新立方體的頂點著色器：

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
...

既然我們已經為每個頂點添加了法線向量並更新了頂點著色器，那麼我們也應該更新頂點屬性指標。請注意，光源的立方體使用相同的頂點陣列作為其頂點資料，但燈光著色器不需要新添加的法線向量。我們不必更新燈光的著色器或屬性配置，但我們至少必須修改頂點屬性指標以反映新頂點陣列的大小：

glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);

我們只想使用每個頂點的前 3 個浮點數，並忽略後 3 個浮點數，所以我們只需要將步長參數更新為 6 乘以 float 的大小即可完成。

燈光著色器沒有完全使用到的頂點資料，這看起來可能效率不高，但頂點資料已經從容器物件儲存在 GPU 的記憶體中，所以我們不需要將新資料儲存到 GPU 的記憶體中。與專門為燈光分配新的 VBO 相比，這實際上更有效率。

所有光照計算都是在片段著色器中完成的，所以我們需要將法線向量從頂點著色器轉發到片段著色器。讓我們來做：

out vec3 Normal;

void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    Normal = aNormal;
}

剩下要做的就是在片段著色器中宣告對應的輸入變數：

in vec3 Normal;

计算漫反射光（Calculating the diffuse color）

我們現在每個頂點都有法線向量，但我們仍然需要光源的位置向量和片段的位置向量。由於光源位置是一個單一的靜態變數，我們可以在片段著色器中將其宣告為 uniform：

uniform vec3 lightPos;

然後在渲染迴圈中更新 uniform（或者在外部，因為它不會每幀改變）。我們使用前一章中宣告的 lightPos 向量作為漫射光源的位置：

lightingShader.setVec3("lightPos", lightPos);

最後我們需要的是片段的實際位置。我們將在世界空間中進行所有光照計算，因此我們首先需要一個在世界空間中的頂點位置。這可以透過將頂點位置屬性僅與模型矩陣相乘（而不是視圖和投影矩陣）來實現，將其轉換為世界空間座標。這可以在頂點著色器中輕鬆實現，所以讓我們宣告一個輸出變數並計算其世界空間座標：

out vec3 FragPos;
out vec3 Normal;

void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    FragPos = vec3(model * vec4(aPos, 1.0));
    Normal = aNormal;
}

最後，將相應的輸入變數添加到片段著色器中：

in vec3 FragPos;

這個 in 變數將從三角形的 3 個世界位置向量中插值，形成 FragPos 向量，即每個片段的世界位置。現在所有必需的變數都已設定，我們可以開始光照計算了。

我們需要計算的第一件事是光源和片段位置之間的方向向量。從上一節我們知道，光的行進方向向量是光源位置向量和片段位置向量之間的差向量。您可能還記得座標轉換章節中，我們可以透過將兩個向量相減來輕鬆計算這個差值。我們還希望確保所有相關向量最終都是單位向量，因此我們對法線和結果方向向量都進行正規化：

vec3 norm = normalize(Normal);
vec3 lightDir = normalize(lightPos - FragPos);

在計算光照時，我們通常不關心向量的長度或它們的位置；我們只關心它們的方向。因為我們只關心它們的方向，所以幾乎所有的計算都是用單位向量完成的，因為它簡化了大多數計算（例如點積）。因此，在進行光照計算時，請確保始終正規化相關向量，以確保它們是實際的單位向量。忘記正規化向量是一個常見的錯誤。

接下來，我們需要透過計算 norm 和 lightDir 向量之間的點積來計算光線對當前片段的漫反射影響。然後將結果值乘以光的顏色以獲得漫反射分量，導致兩個向量之間角度越大，漫反射分量越暗：

float diff = max(dot(norm, lightDir), 0.0);
vec3 diffuse = diff * lightColor;

如果兩個向量之間的角度大於 90 度，那麼點積的結果實際上會變成負數，我們最終會得到一個負的漫反射分量。因此，我們使用 max 函數，它返回兩個參數中較高的那個，以確保漫反射分量（以及顏色）永遠不會變為負數。負顏色的光照沒有明確定義，所以最好避免這種情況，除非您是那些離經叛道的藝術家之一。

現在我們有了環境光和漫反射分量，我們將兩種顏色相加，然後將結果乘以物體的顏色，以獲得最終的片段輸出顏色：

vec3 result = (ambient + diffuse) * objectColor;
FragColor = vec4(result, 1.0);

如果您的應用程式（和著色器）編譯成功，您應該會看到類似這樣的內容：

您可以看到，透過漫反射光照，立方體開始再次看起來像一個實際的立方體。試著在腦海中想像法線向量，並圍繞立方體移動攝影機，看看法線向量與光線方向向量之間角度越大，片段就越暗。

如果您遇到困難，請隨時將您的原始碼與此處的完整原始碼進行比較。

最后一件事

在上一節中，我們將法線向量直接從頂點著色器傳遞到片段著色器。然而，片段著色器中的所有計算都是在世界空間中完成的，那麼我們是不是也應該將法線向量轉換到世界空間座標呢？基本上是的，但它不像簡單地將其與模型矩陣相乘那麼簡單。

首先，法線向量只是方向向量，不代表空間中的特定位置。其次，法線向量沒有齊次座標（頂點位置的 w 分量）。這意味著平移不應該對法線向量產生任何影響。所以如果我們想將法線向量與模型矩陣相乘，我們需要透過取模型矩陣的左上角 3x3 矩陣來移除矩陣的平移部分（請注意，我們也可以將法線向量的 w 分量設定為 0 並與 4x4 矩陣相乘）。

其次，如果模型矩陣執行非均勻縮放，頂點將會以這樣的方式改變，使得法線向量不再垂直於表面。下圖顯示了這種模型矩陣（帶有非均勻縮放）對法線向量的影響：

每當我們應用非均勻縮放時（注意：均勻縮放只會改變法線的長度，不會改變其方向，這很容易透過正規化來解決），法線向量就不再垂直於相應的表面，這會扭曲光照。

解決此行為的技巧是使用專門為法線向量量身定制的不同模型矩陣。這個矩陣稱為法線矩陣，它使用一些線性代數運算來消除錯誤縮放法線向量的影響。如果您想知道這個矩陣是如何計算的，我建議閱讀這篇文章：http://www.lighthouse3d.com/tutorials/glsl-tutorial/the-normal-matrix/。

法線矩陣定義為「模型矩陣左上角 3x3 部分的逆的轉置」。哇，這真是繞口，如果您不太明白這是什麼意思，別擔心；我們還沒有討論逆矩陣和轉置矩陣。請注意，大多數資源將法線矩陣定義為從模型-視圖矩陣導出，但由於我們在世界空間中工作（而不是在視圖空間中），我們將從模型矩陣導出它。

在頂點著色器中，我們可以使用頂點著色器中的 inverse 和 transpose 函數來生成法線矩陣，這些函數適用於任何矩陣類型。請注意，我們將矩陣轉換為 3x3 矩陣，以確保它失去其平移屬性，並且可以與 vec3 法線向量相乘：

Normal = mat3(transpose(inverse(model))) * aNormal;

反轉矩陣對於著色器來說是一個耗費資源的操作，因此盡可能避免執行反轉操作，因為它們必須在場景中的每個頂點上完成。出於學習目的，這沒有問題，但對於高效的應用程式，您可能會希望在 CPU 上計算法線矩陣，並在繪製之前透過 uniform 將其發送到著色器（就像模型矩陣一樣）。

在漫反射光照部分，光照效果很好，因為我們沒有對物體進行任何縮放，所以沒有真正需要使用法線矩陣，我們可以直接將法線與模型矩陣相乘。但是，如果您正在進行非均勻縮放，那麼將法線向量與法線矩陣相乘是必不可少的。

鏡面反射光（Specular Lighting）

如果您還沒有因為所有關於光照的討論而感到筋疲力盡，那麼我們可以透過添加鏡面高光來完成 Phong 光照模型。

與漫反射光照類似，鏡面光照基於光的行進方向向量和物體的法線向量，但這次它還基於視圖方向，例如玩家從哪個方向看向片段。鏡面光照基於表面的反射特性。如果我們將物體表面視為一面鏡子，那麼鏡面光照在我們能看到光線在表面上反射的地方最強烈。您可以在下圖中看到這種效果：

我們透過將光的行進方向圍繞法線向量反射來計算反射向量。然後我們計算這個反射向量與視圖方向之間的角度距離。它們之間的角度越接近，鏡面光的影響就越大。最終的效果是，當我們看向透過表面反射的光線方向時，我們會看到一些高光。

視圖向量是我們用於鏡面光照的額外變數，我們可以利用觀察者的世界空間位置和片段的位置來計算它。然後我們計算鏡面光的強度，將其與光的顏色相乘，並將其添加到環境光和漫反射分量中。

我們選擇在世界空間中進行光照計算，但大多數人更喜歡在視圖空間中進行光照計算。視圖空間的優點是觀察者的位置始終位於 (0,0,0)，因此您已經免費獲得了觀察者的位置。然而，我發現為了學習目的，在世界空間中計算光照更直觀。如果您仍然想在視圖空間中計算光照，您還需要使用視圖矩陣轉換所有相關向量（不要忘記也更改法線矩陣）。

為了獲得觀察者的世界空間座標，我們只需獲取攝影機物件的位置向量（當然，它就是觀察者）。因此，讓我們向片段著色器添加另一個 uniform 並將攝影機位置向量傳遞給著色器：

uniform vec3 viewPos;

lightingShader.setVec3("viewPos", camera.Position);

現在我們已經擁有了所有必需的變數，我們可以計算鏡面強度。首先我們定義一個鏡面強度值，給予鏡面高光一個中等亮度顏色，使其影響不會太大：

float specularStrength = 0.5;

如果我們將其設定為 1.0f，我們會得到一個非常亮的鏡面分量，這對於一個珊瑚立方體來說有點太多了。在下一個章節中，我們將討論如何正確設定所有這些光照強度以及它們如何影響物件。接下來，我們計算視圖方向向量以及沿法線軸的相應反射向量：

vec3 viewDir = normalize(viewPos - FragPos);
vec3 reflectDir = reflect(-lightDir, norm);

請注意，我們對 lightDir 向量取反。reflect 函數期望第一個向量從光源指向片段位置，但 lightDir 向量目前指向相反的方向：從片段指向光源（這取決於我們計算 lightDir 向量時較早的減法順序）。為了確保我們獲得正確的 reflect 向量，我們首先對 lightDir 向量取反來反轉其方向。第二個參數期望一個法線向量，所以我們提供正規化的 norm 向量。

然後剩下要做的是實際計算鏡面分量。這透過以下公式完成：

float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
vec3 specular = specularStrength * spec * lightColor;

我們首先計算視圖方向和反射方向之間的點積（並確保它不是負數），然後將其提高到 32 次方。這個 32 值是高光的發光值。物體的發光值越高，它就越能正確地反射光線而不是將其散射開來，因此高光就越小。下面您可以看到一張顯示不同發光值視覺影響的圖像：

我們不希望鏡面分量太過分散注意力，所以我們將指數保持在 32。剩下唯一要做的是將它添加到環境光和漫反射分量中，然後將組合結果乘以物體的顏色：

vec3 result = (ambient + diffuse + specular) * objectColor;
FragColor = vec4(result, 1.0);

我們現在已經計算了 Phong 光照模型的所有光照分量。根據您的視角，您應該會看到類似這樣的內容：

您可以在此處找到應用程式的完整原始碼。

在早期光照著色器中，開發人員習慣於在頂點著色器中實現 Phong 光照模型。在頂點著色器中進行光照的優點是它效率更高，因為通常頂點比片段少得多，因此（昂貴的）光照計算頻率較低。然而，頂點著色器中的結果顏色值僅是該頂點的結果光照顏色，周圍片段的顏色值是插值光照顏色的結果。結果是光照不夠真實，除非使用大量頂點：

當 Phong 光照模型在頂點著色器中實現時，它被稱為 Gouraud 著色而不是 Phong 著色。請注意，由於插值，光照看起來有些偏差。Phong 著色給出了更平滑的光照結果。

到目前為止，您應該已經開始看到著色器有多麼強大。僅憑少量資訊，著色器就能計算出光照如何影響所有物件的片段顏色。在接下來的章節中，我們將更深入地探討光照模型的功能。