我們現在知道如何創建物件,為它們上顏色,以及如何使用紋理為它們的外觀填充細節。然而,它們至今還是有些無趣,因為它們都是靜止的。我們將嘗試一種新的作法,通過在每一個幀修改它們的頂點以及對它們的緩衝數據進行重新配置來使它們“動”起來,然爾這似乎是一件繁重的任務,同時也會消耗相當多的處理資源。存在一種更好的辦法以變換一個物件,就是使用一個或者多個矩陣對象。這不意味著我們將討論功夫或者什麼數字人工世界之類的玩意。
矩陣是一種非常強大的數學工具,雖然它初一看上去有些恐怖,但只要你對它們逐漸熟悉,它們將變得非常有用。當我們討論矩陣的時候,我們必須稍微深入地去了解一點數學知識。針對那些對數學更有興趣的讀者,我將補充材料放在文章的最後以供你們擴展閱讀。
然爾,要完全掌握變換(transformation),在討論矩陣之前,我們首先還必須深入地了解一下向量。這一章的核心關注點是給予你一些基礎的數學知識,以備後續之用。如果主題有些複雜,嘗試儘可能多地去理解,後邊任何時候,如果你需要重新溫習這些概念和知識,可以回到這一章再看看。
向量
就大部分基本定義來說,向量就是一些“方向”,再無別的什麼含義。一個向量有一個方向以及一個量(也被稱為強度或著長度)。你可以將向量想像為“藏寶圖”上的指引箭頭:“向左行 10 步,現在,向北行 3 步,然後向右行 5 步”;這裡,“左”就是方向,爾“10 步”就是這個向量的大小。藏寶圖上因此有 3 個向量。向量可以具備任意多的緯度,但我們通常使用 2 到 4 維。如果一個向量有 2 維,它就可以表示平面(想想一個 2D 圖)上的一個方向,爾當它有 3 個緯度的時候,它可以表示 3D 世界的任意方向。
以下,我們看到 3 個向量,每一個都使用 $(x,y)$ 表示 2D 圖上的一個箭頭。由於在 2D 空間顯示向量比在 3D 要更直觀,你可以將 2D 向量看作 $z=0$ 情况下的 3D 向量。因為向量表示方向,其起點不會改變它的值。在下圖中,我們可以看到向量 $\vec{v}$ 和 $\vec{w}$ 是相等的,雖然它們的起始點不同。
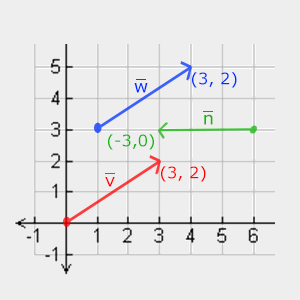
當描述向量的時候,數學家更喜歡將它們表述為一個字符符號,使用一個帽子,像這樣 $\vec{v}$。同時,當在公式裡書寫向量的時候,它們通常寫成這樣:
\vec{v}=\begin{pmatrix}
x\\
y\\
z\\
\end{pmatrix}
由於向量被定義為方向,有時候很難像位置那样對它們進行可視化。如果我們要將它們按照位置的方式進行可視化,我們可以將它們的起點設想為 $(0,0,0)$,然後指向一個特定的方向,使得它成為一個位置向量(我們也可以指定一個不同的起點,然後說:這個向量從此起點出發指向空間中的那個點)。這樣,位置向量 $(3,5)$ 就可以在圖上指向 $(3,5)$,它的起點是 $(0,0)$。使用向量,我們就可以在 2D 和 3D 空間裡描述方向和位置。
和普通的數一樣,我們也可以為向量定義若干操作方法(其中有些你已經了解)。
標量/向量操作(Scalar/Vector Operations)
標量,是一個單體數字。當使一個向量對一個標量執行加/減/乘或著除的操作,我們簡單地對向量的每一個分量執行這些“標量”操作。對于“加”,它看上去就是:
{\begin{pmatrix}
1\\
2\\
3\\
\end{pmatrix}} + x
\rightarrow
{\begin{pmatrix}
1\\
2\\
3\\
\end{pmatrix}} +
{\begin{pmatrix}
x\\
x\\
x\\
\end{pmatrix}}
=
{\begin{pmatrix}
1 + x\\
2 + x\\
3 + x\\
\end{pmatrix}}
這裡,$+$ 可以是 $+$ ,$-$ ,$\cdot$ 或著 $\div$,其中 $\cdot$ 是乘法運算。
向量取反(Vector negation)
將一個向量取反,得到另一個向量,它和原向量方向相反。比如,一個向量指向東北,取反之後,它將指向西南。要對一個向量取反,我們對其每一個分量加負號(我們也可以將其表述為一個標量-向量的乘法操作,乘 -1 即可):
-{\vec v} =
-{\begin{pmatrix}
v_x\\
v_y\\
v_z\\
\end{pmatrix}}
=
{\begin{pmatrix}
-v_x\\
-v_y\\
-v_z\\
\end{pmatrix}}
加法和減法
對兩個向量執行加法,被定義為,對向量的每個分量執行加法操作,也就是,使向量的每個分量加上另一個向量的同等分量,就像:
{\vec v}=
{\begin{pmatrix} 1\\ 2\\ 3\\ \end{pmatrix}},
{\vec k}=
{\begin{pmatrix} 4\\ 5\\ 6\\ \end{pmatrix}}
\rightarrow
{\vec v} + {\vec k}=
{\begin{pmatrix} 1+4\\ 2+5\\ 3+6\\ \end{pmatrix}}
=
{\begin{pmatrix} 5\\ 7\\ 9\\ \end{pmatrix}}
視覺效果上來看,下圖看起來像是向量 $\vec{v}=(4,2)$ 和 $\vec{k}=(1,2)$ 的相加,其中第二個向量從第一個向量的終點開始接續,藉此找出結果向量的終點位置(這就是「首尾相接法」)。
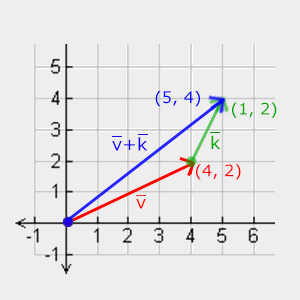
和常規的加法、減法一樣,向量的減法就是對取反後的第二個向量執行加法運算:
{\vec v}=
{\begin{pmatrix} 1\\ 2\\ 3\\ \end{pmatrix}},
{\vec k}=
{\begin{pmatrix} 4\\ 5\\ 6\\ \end{pmatrix}}
\rightarrow
{\vec v} + -{\vec k}=
{\begin{pmatrix} 1+(-4)\\ 2+(-5)\\ 3+(-6)\\ \end{pmatrix}}
=
{\begin{pmatrix} -3\\ -3\\ -3\\ \end{pmatrix}}
兩個向量相減得到一個新向量,它是兩個向量所指位置的差。在我們需要獲取一個向量,并希望它是兩個位置之差時,這種方式非常有用。
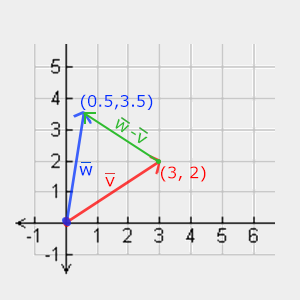
長度
要得到一個向量的長度/大小,我們使用 Pythagoras 理論,這個理論你或許在你的數學課上聽說過。當你將一個向量的 x 和 y 分量視為兩個邊,它會形成一個三角形:
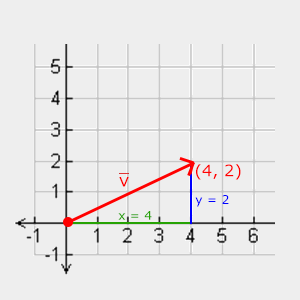
由於兩個邊 $(x, y)$ 的長度已知,我們需要知道標記以 $\vec{v}$ 的這條邊的長度,可以使用 Pythagoras 理論計算:
\lVert{\vec{v}}\rVert={\sqrt{x^2 + y^2}}
這裡,$\lVert{\vec{v}}\rVert$ 表示向量 $\vec{v}$ 的長度。通過向此算式加上 $z^2$,很容易將其擴展為 3D 的情境。這個例子中,向量 $(4, 2)$ 的長度等於:
\lVert{\vec{v}}\rVert=
{\sqrt{4^2 + 2^2}}
=
{\sqrt{16 + 4}}
={\sqrt{20}}
=4.47
結果是 4.47。
有一種特殊向量,我們稱為單位向量。一個單位向量較普通向量有一個額外的屬性,那就是它的長度剛好是 1。我們可以通過對向量的三個分量除以此向量的長度,得到它的單位向量 $\hat{n}$。
\hat{n}
=
\frac{\vec{v}}{\lVert{\vec{v}}\rVert}
我們將這個操作稱為“向量單位化”。單位向量的寫法是在其頭頂加一個帽子。它們通常很有用處,特別是在我們只關注向量方向時(我們改變向量的長度,其方向始終保持不變)。
向量-向量乘法(Vector-vector multiplication)
兩個向量的乘法有些奇怪。常規的乘法並未在向量操作裡定義,因為它不具備視覺上的意義,但是有兩種乘法可供我們選擇:其一是 dot product,表述為 $\vec{v} \cdot \vec{k}$,另一個是 cross product,表述為 $\vec{v} \times \vec{k}$。
點積(Dot product)
兩個向量的點積結果等於它們長度的標量之積,再乘以二者之角的 cosine 值。如此聽上去有些困惑,那麼看一下它的公式:
{\vec{v}} \cdot {\vec{k}}
=
{\lVert \vec{v} \rVert}
\cdot
{\lVert \vec{k} \rVert}
\cdot
\cos{\theta}
其中,二者的夾角使用 theta ($\theta$) 表示。為何這很有趣呢?好,設想一下,如果 $\vec{v}$ 和 $\vec{k}$ 是單位向量,那麼它們的長度將會是 1。這可以使得上述公式顯著簡化為:
{\hat{v}} \cdot {\hat{k}}
=
1
\cdot
1
\cdot
\cos{\theta}
=
\cos{\theta}
現在,點積只定義了兩個向量的夾角。你或許記得,當角度是 90 度的時候,其 cosine 或著 cos 值為 0,當角度為 0 的時候,其值為 1。使用點積讓我們可以很輕鬆地測試出兩個向量是正交或者平行 (正交的意思是兩個向量的夾角為直角)。如果你想對 sin 和 cos 函數有更多的了解,我建議你去追尋 Khan Academy videos 裡關於“三角幾何”部分。
你也可以計算兩個非單位向量的夾角,不過你需要對結果除以兩個向量的長度,使其只剩下 $\cos{\theta}$。
那麼,我們該如何計算點積呢?點積的計算是將向量的每一個分量進行相乘,然後將它們加起來。對於兩個單位向量,這看上去就是(你可以驗證一下它們的長度是否都剛好是 1):
{\begin{pmatrix}
0.6\\
-0.8\\
0\\
\end{pmatrix}}
\cdot
{\begin{pmatrix}
0\\
-1\\
0\\
\end{pmatrix}}
=
(0.6 \times 0)
+
(-0.8 \times 1)
+
(0 \times 0)
=
-0.8
為了計算二者的夾角,我們使用 cosine 函數的逆函數 $\cos^{-1}$,它計算的結果是 143.1 度。我們現在成功地計算出了這兩個向量的夾角。點積在進行後邊的光線計算時非常有價值。
叉積(Cross product)
叉積的定義是,在 3D 空間,它使用兩個向量作為輸入,然後產生第三個向量,它與輸入的兩個向量均呈正交關係。如果兩個輸入向量也是正交關係,那麼三個向量相互正交;這在後續的章節裡非常有用。下圖顯示出這種計算在 3D 空間裡的呈現:
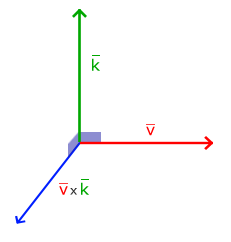
和其它操作不同的是,叉積不那麼直觀,除非你深入研究一下線性代數相關知識,因此最好就是記下這個公式,這樣沒有問題(或著不記住它,那麼沒啥關係)。以下,你將看到兩個正交向量 A 和 B 的叉積:
\begin{pmatrix}
A_x\\
A_y\\
A_z\\
\end{pmatrix}
\times
\begin{pmatrix}
B_x\\
B_y\\
B_z\\
\end{pmatrix}
=
\begin{pmatrix}
A_y \cdot B_z - A_z \cdot B_y \\
A_z \cdot B_x - A_x \cdot B_z \\
A_x \cdot B_y - A_y \cdot B_x \\
\end{pmatrix}
如你所見,這似乎沒啥意義。然爾,如果你僅僅按照這些步驟去做,你可以得到一個與你所輸入向量均正交的一個向量。
矩陣(Matrices)
現在,我們已經討論了幾乎全部的向量相關的內容,是時候進入到矩陣主題了。矩陣是一個數字的矩形陣列,一種符號,或著一種數學表達。其中的每一項被稱為矩陣的“元素”。一個 $2\times3$ 矩陣的例子如下:
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{bmatrix}
矩陣以 $(i, j)$ 為索引,這裡 i 表示行序號,j 表示列序號,這就是為什麼它被稱為 $2 \times 3$ 矩陣 (3 列 2 行,也被稱為矩陣的緯度)。這和你在 2D 圖中所使用的索引——比如 $(x, y)$——是相反的。要獲得數字 4,我們會將使用索引值 $(2,1)$(第二行,第一列)。
矩陣也就是如此,沒有更多,僅僅是一個數學表達上的矩形陣列。它們當然也有一套非常漂亮的數學屬性,就像向量那樣,我們可以針對矩陣定義若干操作,叫做:加法、減法以及乘法。
加法和減法(Addition and subtraction)
矩陣的加法和減法用於兩個矩陣之間,分別對每一個元素進行加減操作。所以,我們熟悉的普通數字運算規則同樣適用,只是運算是針對兩個矩陣中具有相同索引的位置元素進行的。這也意味著加減操作只針對相同緯度的矩陣。一個 $3 \times 2$ 的矩陣和一個 $2 \times 3$ 的矩陣是不可能被加減到一起的。讓我們來看看兩個 $2 \times 2$ 的矩陣的加法是如何進行的:
\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ {10} & {12} \end{bmatrix}
矩陣減法遵循相同的規則:
\begin{bmatrix} 4 & 2 \\ 1 & 6 \end{bmatrix} - \begin{bmatrix} 2 & 4 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 4 - 2 & 2 - 4 \\ 1 - 0 & 6 - 1 \end{bmatrix} = \begin{bmatrix} 2 & -2 \\ 1 & 5 \end{bmatrix}
矩陣-標量乘積(Matrix-scalar products)
矩陣-標量的積的計算是,對每一個矩陣元素乘以這個標量。以下的例子演示了這種乘法:
{2} \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} {2} \cdot 1 & {2} \cdot 2 \\ {2} \cdot 3 & {2} \cdot 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}
現在我們也能理解,為什麼那些單一的數字會被稱為「標量」(scalar in English)。一個標量本質上可以對矩陣的全部元素進行“縮放”(scales)。上一個例子中,全部元素都被放大了 2 倍。
到目前為止一切都還算簡單,情況都不算太複雜。但這情況會改變,當我們開始進入矩陣與矩陣的相乘時就不一樣了。
矩陣-矩陣乘法(Matrix-matrix multiplication)
對矩陣進行乘法運算不必然是複雜的,但是要習慣它稍稍困難。矩陣的乘法本質上遵循了一系列預定義的規則。但有幾個限制:
- 只有当當邊矩陣的列數和右邊矩陣的行數一致,你才能對兩個矩陣進行乘法運算。
- 矩陣的乘法不遵循交換律,也就是 $A \cdot B \neq B \cdot A$。
我們使用兩個 $2\times2$ 的矩陣的乘法作為例子:
\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \cdot \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 1 \cdot 5 + 2 \cdot 7 & 1 \cdot 6 + 2 \cdot 8 \\ 3 \cdot 5 + 4 \cdot 7 & 3 \cdot 6 + 4 \cdot 8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}
現在,或許你正嘗試理解其中發生了什麼?矩陣乘法是一種將一般的乘法與加法結合起來的運算方式,它是使用左邊矩陣的行與右邊矩陣的列進行運算的。讓我們根據下圖進一步討論:

我們首先取左邊矩陣的頭部的行,然後取右邊矩陣的一列。我們選擇的行和列決定了 $2\times2$ 結果矩陣中的我們要計算的那個值。如果我們取左側矩陣的第一行,計算的值將落在結果矩陣的第一行,然後我們取一列,如果是第一列,計算的值將落在結果矩陣的第一列。這正是“紅色路徑”的情況。要計算右下角的值,我們取第一個矩陣的最後一行和第二個矩陣的最後一列。
要計算出最終的值,我們對行和列的值進行普通的乘法運算,然後對第二個元素進行一樣的計算,接著是第三、第四個,如此等等。單個乘法的結果最後求和,我們拿到了結果。現在我們終於明白,為什麼左側矩陣的列和右側矩陣的行的大小必須一致,否則我們無法完成運算。
結果我們得到了這樣的一個矩陣,它的緯度是 $(n,m)$,其中 n 和左側矩陣的行數相等,爾 m 和右側矩陣的列數相等。
如果你對腦算其中的乘法感到些許困難,不要擔心,你可以手動去完成計算,然後在你遇到困難的時候,回來再看看這篇文章。隨著時間推移,矩陣的乘法運算對與你會變為次自然的一件事。
讓我們使用一個更複雜的例子來結束對矩陣-矩陣的乘法運算的討論吧。試著對這個計算方式進行可視化,可以藉助顏色。作為一種有效的練習,來看看你是否可以計算出自己的答案,然後將其和我們的結果矩陣比較一下(一旦你嘗試手動完成矩陣的乘法運算,你將很快掌握它們)。
\begin{bmatrix} 4 & 2 & 0 \\ 0 & 8 & 1 \\ 0 & 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 4 & 2 & 1 \\ 2 & 0 & 4 \\ 9 & 4 & 2 \end{bmatrix} = \begin{bmatrix} 4 \cdot 4 + 2 \cdot 2 + 0 \cdot 9 & 4 \cdot 2 + 2 \cdot 0 + 0 \cdot 4 & 4 \cdot 1 + 2 \cdot 4 + 0 \cdot 2 \\ 0 \cdot 4 + 8 \cdot 2 + 1 \cdot 9 & 0 \cdot 2 + 8 \cdot 0 + 1 \cdot 4 & 0 \cdot 1 + 8 \cdot 4 + 1 \cdot 2 \\ 0 \cdot 4 + 1 \cdot 2 + 0 \cdot 9 & 0 \cdot 2 + 1 \cdot 0 + 0 \cdot 4 & 0 \cdot 1 + 1 \cdot 4 + 0 \cdot 2 \end{bmatrix}
= \begin{bmatrix} 20 & 8 & 12 \\ 25 & 4 & 34 \\ 2 & 0 & 4 \end{bmatrix}
如你所見,矩陣-矩陣乘法運算是一種相對複雜的過程,而且非常容易出錯(這也是為什麼我們通常讓計算機來做這件事),而且隨著矩陣變大,問題的出現也會更明顯。如果你渴望了解更多的相關知識,並且你對其更多的數學特徵感到好奇,我強烈推薦你看看這些講解矩陣的教學視頻。
總之,我們已經知道如何對矩陣做乘法運算了,接下來要開始討論一些有趣的內容。
矩陣-向量乘法(Matrix-Vector multiplication)
截止目前,我們已經接觸了不少的向量。我們使用它們來表示位置、顏色,甚至是紋理座標。讓我們再進一步,我告訴你向量其實本質上是一個 $N \times 1$ 矩陣,其中 N 是向量的分量數目(也被稱為 N 維向量)。如果你想一下,就會發現這其實是有道理的。向量其實和矩陣一樣,是一個數字排列,但是只有 1 列。那麼,這一信息對我們有什麼幫助呢?好,如果我們有一個 $M \times N$ 的矩陣,我們將它和一個 $N \times 1$ 的向量做乘法運算,由於矩陣的列數和向量的行數一致,矩陣乘法是合法的。
然而,為什麼我們關注這個問題,即我們能否將一個矩陣乘以一個向量?是這樣的,之所以如此,因為存在大量有趣的 2D/3D 轉換可以依賴矩陣實現,讓矩陣乘以一個向量將對這個向量加以轉換。如果你依然對此有些許困惑,讓我們拿出幾個例子來,你將很快明白我們說的是什麼意思。
單位矩陣(Identity matrix)
在 OpenGL 當中,我們常常會和 $4 \times 4$ 的轉換矩陣打交道,這裡涉及一些背景,其中之一就是絕大多數向量都是 4 維的。最最簡單的轉換矩陣,我們能夠馬上想到的,就是單位矩陣。單位矩陣是一個 $N \times N$ 的矩陣,除了對角線上的數字,其餘元素全是 0。如你即將看到的,這樣的矩陣對向量完全沒有作用(不會改變向量)。
\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} = \begin{bmatrix} 1 \cdot 1 \\ 1 \cdot 2 \\ 1 \cdot 3 \\ 1 \cdot 4 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}
向量完全沒有改變。根據矩陣乘法規則,這顯而易見:結果裡的第一個元素為矩陣第一行的每一個元素和向量的每一個元素相乘得到的。由於矩陣第一行裡的元素除了第一個之外全部為 0,我們得到 $1\cdot1+0\cdot2+0\cdot3+0\cdot4=1$,向量的其餘三個元素應用相同的計算辦法。
你或許會感到好奇,這樣一種對向量不做任何轉化的矩陣有什麼用處呢?單位矩陣通常用於生成其它轉換矩陣,如果我們能夠更加深入地了解線性代數,它是一個非常有用的矩陣,用於證明理論以及解決線性方程。
縮放(Scaling)
當我們縮放一個向量的時候,我們增加其長度以一個我們想要的量,爾方向保持不變。由於我們在二維或者三維空間操作,因此我們可以使用一個包含 2 個或者 3 個縮放因子的向量,使每個分量沿著對應的軸進行縮放。
讓我們來對向量 $\vec{v}=(3,2)$ 進行縮放。我們將沿著 x 軸對其縮放 0.5 倍,即使其變窄一半。然後,我們沿著 y 軸縮放 2 倍,即使其變高一倍。我們來看看對向量縮放 $\vec{s} = (0.5,2)$ 之後的樣子:
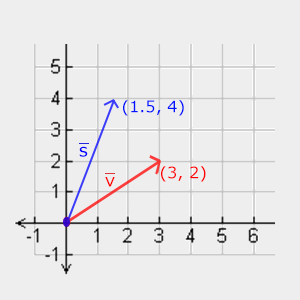
記住,OpenGL 通常是針對 3D 空間操作的,因此對於這種 2D 的情況,我們可以設置 z 軸方向的縮放因子為 1,這對結果沒有任何影響。我們方才執行的縮放操作是一個非均勻縮放縮放,因為縮放因子在各個軸上不相等。如果縮放因子於三個軸線相等,那麼我們可以將這樣的縮放稱為均勻縮放。
我們開始構建一個轉換矩陣,用它來為我們做縮放操作。我們從單位矩陣看到過,對角線上的每一個元素會和對應的向量元素做乘法。如果我們將單位矩陣中的 1s 修改為 3s 會怎麼樣呢?那種情況下,我們將對每個向量元素乘以 3,因此這相當於將向量放大了 3 倍。如果我們將縮放因子表述為 $(S_1,S_2,S_3)$,可以將一個作用於任意向量 $(x,y,z)$ 的縮放矩陣定義為:
\begin{bmatrix} {S_1} & 0 & 0 & 0 \\ 0 & {S_2} & 0 & 0 \\ 0 & 0 & {S_3} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} {S_1} \cdot x \\ {S_2} \cdot y \\ {S_3} \cdot z \\ 1 \end{pmatrix}
注意,我們始終將第四個縮放因子設置為 1,w 分量用於其它用途,我們稍後會了解。
平移(Translation)
平移是這樣一種操作,它將另一個向量加到原向量的尾部,然後返回一個新的向量,得到一個不同的位置,於是實現了基於一個平移向量來 移動 一個向量的效果。我們已經討論過向量的加法,這應該不算太新鮮吧?
就像縮放矩陣,對於一個 $4 \times 4$ 矩陣,有幾個位置可以讓我們用來執行某種操作,對於平移,它們是第四列的前三個值。如果我們將平移向量表述為 $(T_x,T_y,T_z)$,我可以將平移矩陣定義為這樣:
\begin{bmatrix} 1 & 0 & 0 & {T_x} \\ 0 & 1 & 0 & {T_y} \\ 0 & 0 & 1 & {T_z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + {T_x} \\ y + {T_y} \\ z + {T_z} \\ 1 \end{pmatrix}
這是有效的,因為全部的平移值都會被向量的 w 列,並且加到向量的原始值上(回憶一下,這是矩陣乘法規則)。這並不適用於 $3 \times 3$ 矩陣。
齊次座標(Homogeneous coordinates)
向量的 w 分量也被稱為齊次座標。要從一個齊次向量得到一個 3D 向量,我們將 x、y、z 除以它的 w 座標。我們通常沒有注意這個這點,因為 w 分量大部分時候都是 1。使用齊次座標有幾個好處:它允許我們對 3D 向量(沒有 w 分量,我們無法平移向量)執行矩陣的平移操作,下一章,我們將使用 w 分量創建 3D 透視。
同時,如果齊次座標為 0,那麼向量被特指方向向量,因為 w 為 0 的的向量無法被平移。
藉助平移矩陣,我們可以沿著三個軸 $(x, y, z)$ 的方向移動物件,使它成為轉換操作中非常有用的一種矩陣。
旋轉(Rotation)
上面幾個轉換相對比較容易理解,也容易在 2D 或 3D 空間可視化,但是旋轉會顯得要特別一點。如果你想知道這些矩陣是如何被構造出來的,我建議你去看看這些和旋轉相關的視頻教程。
首先,讓我們定義好究竟什麼是向量的旋轉。在 2D 或 3D 空間下,一個旋轉伴隨著一個角度。角度可以是以“度數”為單位,或者是以“弧度”為單位,其中一整個圈將是 $360^\circ$ 或者 $2\pi$ 個弧度。我傾向於使用“度數”來解釋旋轉,鑒於我們一般對它更熟悉一些。
大多數的旋轉函數需要一個弧度角,但是好在從度數到弧度的轉換很簡單:
angle in degrees = angle in radians * (180 / PI)
angle in radians = angle in degrees * (PI / 180)
其中 PI (四捨五入)等於 3.14159265359。
旋轉半個圈意為旋轉 360/2 = 180 度,爾向右旋轉 1/5th 意為向右旋轉 360/5 = 72 度。以下演示了一個 2D 向量 $\vec{v}$ 由 $\vec{k}$ 向右(順時針)旋轉 72 度的效果。
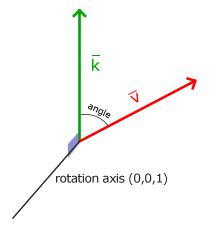
3D 空間裡的旋轉被指定為一個角度加上一個旋轉軸,角度被指定為物件圍繞旋轉軸旋轉的角度。嘗試想像這個情境:讓你的頭沿著某個旋轉軸持續看著某個方向,同時轉動一定的角度。在 3D 空間旋轉 2D 向量,我們將旋轉軸設置為 z 軸(試著想像一下畫面)。
使用三角函數,將向量轉換為旋轉某個角度後的向量是可行的。這通常是根據 sine 和 cosine 函數(術語通常是 sin 和 cos)的結合實現的。對於旋轉矩陣的生成的討論超出了本章的範圍。
旋轉矩陣是在三維空間中的每個單位軸上定義的,旋轉角度通常以希臘字母 $\theta$ (theta) 表示。
圍繞 X 軸的旋轉:
\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & {\cos \theta} & - {\sin \theta} & 0 \\ 0 & {\sin \theta} & {\cos \theta} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ {\cos \theta} \cdot y - {\sin \theta} \cdot z \\ {\sin \theta} \cdot y + {\cos \theta} \cdot z \\ 1 \end{pmatrix}
圍繞 Y 軸的旋轉:
\begin{bmatrix} {\cos \theta} & 0 & {\sin \theta} & 0 \\ 0 & 1 & 0 & 0 \\ - {\sin \theta} & 0 & {\cos \theta} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} {\cos \theta} \cdot x + {\sin \theta} \cdot z \\ y \\ - {\sin \theta} \cdot x + {\cos \theta} \cdot z \\ 1 \end{pmatrix}
圍繞 Z 軸的旋轉:
\begin{bmatrix} {\cos \theta} & - {\sin \theta} & 0 & 0 \\ {\sin \theta} & {\cos \theta} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} {\cos \theta} \cdot x - {\sin \theta} \cdot y \\ {\sin \theta} \cdot x + {\cos \theta} \cdot y \\ z \\ 1 \end{pmatrix}
使用旋轉矩陣,我們可以對位置向量圍繞三個單位軸的任意一個進行轉換。要圍繞一個任意的 3D 軸旋轉,我們可以將此 3 個旋轉組合起來,先繞 X 軸旋轉,然後繞 Y 軸,最後繞 Z 軸。但是,這很快導致了一個問題,就是 Gimbal lock。我們不在此詳細探討這個問題,但是一個好的解決方法是直接繞一個單位軸——比如 $(0.662,0.2,0.722)$ ——旋轉,而非圍繞三個旋轉旋轉。這樣一種(囉嗦的)矩陣是存在的,如下所示,它的旋轉軸是 $(R_x,R_y,R_z)$。
\begin{bmatrix} \cos \theta + {R_x}^2(1 - \cos \theta) & {R_x}{R_y}(1 - \cos \theta) - {R_z} \sin \theta & {R_x}{R_z}(1 - \cos \theta) + {R_y} \sin \theta & 0 \\ {R_y}{R_x} (1 - \cos \theta) + {R_z} \sin \theta & \cos \theta + {R_y}^2(1 - \cos \theta) & {R_y}{R_z}(1 - \cos \theta) - {R_x} \sin \theta & 0 \\ {R_z}{R_x}(1 - \cos \theta) - {R_y} \sin \theta & {R_z}{R_y}(1 - \cos \theta) + {R_x} \sin \theta & \cos \theta + {R_z}^2(1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
生成它的數學相關的討論不在本章的範圍。記住,即便這樣一個矩陣,它也無法完全避免 gimbal lock (儘管它讓問題更加難解)。要真正地不讓 Gimbal locks 產生,我們必須將旋轉表述為四元數(Quaternion),它不但安全,而且對計算更加有好。然爾,關於四元數的討論也不在本章範圍,哈哈。
合併矩陣(Combining matrices)
矩陣真正的厲害之處在於,我們可以根據矩陣的乘法法則,對多個矩陣進行合併,從而形成一個矩陣。讓我們來看看是否真的可以通過合併多個轉換形成一個轉換。比如,我現在有一個向量 $(x,y,z)$,我們想將它縮放 2 倍,然後平移 $(1,2,3)$。要完成這些步驟,我們需要一個平移矩陣和一個縮放矩陣。最後的轉換矩陣看上去是這樣的:
Trans \cdot Scale = \begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 3 \\ 0 & 0 & 0 & 1 \end{bmatrix} . \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 0 & 0 & 1 \\ 0 & 2 & 0 & 2 \\ 0 & 0 & 2 & 3 \\ 0 & 0 & 0 & 1 \end{bmatrix}
注意,在執行矩陣乘法的時候,我們首先做平移,然後做縮放。矩陣的乘法是不遵循交換律的,這也就意味著它們的順序很重要。當對矩陣做乘法運算的時候,最右側的矩陣首先和向量相乘,因此你需要從右向左地去閱讀矩陣乘法。在合併矩陣的時候,建議先執行縮放操作,然後是旋轉,最後是平移;否則它們可能相互產生(不好的)影響。比如,如果你先平移,然後縮放,那麼平移向量也會被縮放。
對我們的向量應用最後的轉換矩陣,得到以下向量:
\begin{bmatrix} 2 & 0 & 0 & 1 \\ 0 & 2 & 0 & 2 \\ 0 & 0 & 2 & 3 \\ 0 & 0 & 0 & 1 \end{bmatrix} . \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} 2x + 1 \\ 2y + 2 \\ 2z + 3 \\ 1 \end{bmatrix}
很好,向量首先被縮放了 2 倍,然後平移 $(1,2,3)$。
應用 (In practice)
現在我們已經對轉換背後的理論進行了解釋,是時候探究一下我們實際如何使用這些知識。OpenGL 不提供任何形式的內置的矩陣和向量功能,因此我們必須定義我們自己的數學類和函數。這本書中,我們不會為那些細微的數學知識抽象出工具、類和函數,而是使用已經寫好的數學庫。幸運的是,有一個容易上手的、也是專為 OpenGL 設計的數學庫,它的名字就是 GLM。
GLM
GLM 的全稱是 OpenGL Mathematics,是一個僅包含頭文件的庫。這個意思是我們只需要包含進正確的頭文件即可,我們已經做了這件事。無需 linking 和編譯。GLM 可以從它們的網站上下載,然後將其整個目錄拷貝到你的 includes 文件夾,開始吧!
我們所需要的多數 GLM 功能可以在這 3 個頭文件裡找到,以下我們將其包含進來:
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
我們看看是否可以將轉換用於將向量 $(1,0,0)$ 平移 $(1,1,0)$(注意我們將向量定義為類型 glm::vec4,它包含了齊次座標,數值為 1.0)。
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;
我們首先定定義了向量,名字為 vec,使用的是 GLM 內置的向量類。然後,我麼定義了一個 mat4,並且直接將其初始化為單位矩陣,並且將對角元素的值設置為 1.0;如果我們不對它進行初始化,那麼它將是一個空矩陣(所有元素的值都是 0),而且接下來的矩陣操作也都將導致一個空矩陣。
接下來,通過傳入這個單位矩陣到函數 glm::translate ,我們創建了一個轉換矩陣,同時傳入一個平移向量(傳入的矩陣會和一個平移矩陣相乘,並將結果返回)。接著,我們將向量乘這個轉換矩陣,輸出平移結果。如果我們還記得平移是如何工作的,最終的向量應該是 $(1+1,0+1,0+0)$,也就是 $(2,1,0)$。這段代碼輸出的結果是 210,因此平移矩陣處理得沒有問題。
讓我們來點有意思的,縮放然後旋轉我們在上一章裡做的盒子。
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));
首先,我們對盒子對每個軸縮放了 0.5,然後繞 z 軸旋轉了 90 度。GLM 需要的是弧度角,因此我們將度數轉化為弧度,這是通過 glm::radians 做到的。注意,我們貼圖後的矩形在 XY 平面,因此我們對 Z 軸旋轉。記住,旋轉所圍繞的軸線必須是單位向量,因此確保在繞 x/y/z 軸旋轉之前,你是首先對其進行了標準化。因為我們將矩陣傳遞給每個 GLM 的函數,GLM 會自動將這些矩陣相乘,從而產生一個合併所有變換的變換矩陣。
接下來的一個大問題是:我們如何讓這個轉換矩陣傳入到 shader?我曾簡單地提到過,GLSL 裡也有一個數據類型 mat4。因此我們可以讓頂點著色器接收一個 mat4 類型的 uniform 變量,然後使其與向量相乘:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;
out vec2 TexCoord;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(aPos, 1.0f);
TexCoord = vec2(aTexCoord.x, aTexCoord.y);
}
GLSL 也有類型 mat2 和 mat3,它們允許我們進行“類-組合”操作,就像向量的組合操作那樣。之前提到的全部的數學操作(像 scalar-matrix 乘法、matrix-vector 乘法,以及 matrix-matrix 乘法)對於 GLSL 的矩陣類型都被允許。凡是使用這兩種矩陣運算的地方,我們都會確保說明其背後的原因。
我們加上了 uniform,並使用轉換矩陣對位置向量做了相乘,最後將位置向量交給 gl_Position。我們的箱子該縮小了一半,並且旋轉了 90 度(向左傾斜)。但我們還需要將轉換矩陣傳入到著色器。
unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));
我們首先查詢了 uniform 變量的位置,然後將 matrix 數據發送給 shader,這裡使用的是 glUniform* 函數,以 Matrix4fv 為函數後綴。第一個參數我們很熟悉,就是 uniform 的位置。第二個參數告訴 OpenGL 我們有幾個矩陣需要傳送,這裡是 1 個。第三個參數問我們是否需要 transpose 我們的矩陣,這個意思是將行和列進行調換。OpenGL 的開發者經常使用一種被稱為“列優先”次序的內部矩陣 layout,這在 GLM 當中是默認的矩陣 layout,因此我們無需 transpose 這些矩陣;我們將其保留為 GL_FALSE。最後一個參數就是實際的矩陣數據了,但 GLM 保存矩陣數據的方式不總是讓 OpenGL 滿意,因此我們首先使用 GLM 內置的函數 value_ptr 將數據進行一次轉換。
我們創建了一個轉換矩陣,在頂點著色器中聲明了一個 uniform,並且將矩陣發送給了著色器,其中我們對頂點座標進行轉換。最後的結果看上去是這樣的:
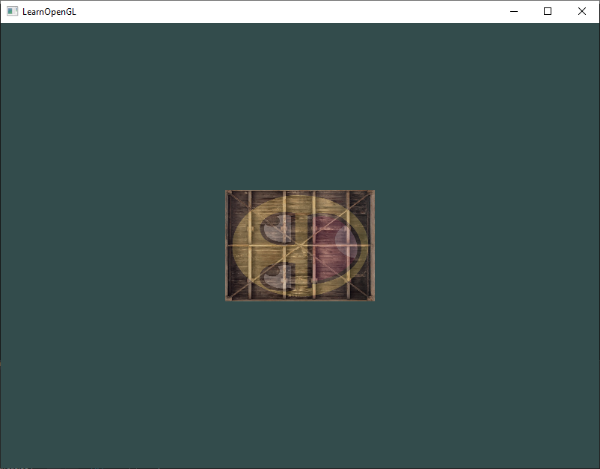
完美!我們箱子現在確實向左側傾斜了,而且比原本縮小了兩倍,這說明轉換是成功的。讓我們來點有趣的,看看我們能否讓箱子隨著時間去旋轉,同時也是為了有點趣味,我們將箱子的位置修改到窗口的右下方。要隨著時間對箱子進行旋轉,我們還必須在渲染循環中不斷更新轉換矩陣,因為它需要在每次渲染的時候更新。我們使用 GLFW 的 time 函數獲取歲時間變化的角度:
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));
記住,在上一個例子中,我們可以在任何地方聲明一個轉換矩陣,但是現在我們必須在渲染函數裡創建它以持續對它更新。這意味著我們必須在每一幀都重新創建一個轉換矩陣。通常來說,當渲染一個場景的時候,我們有若干矩陣需要在每一幀重新創建。
這裡,我們首先將箱子圍繞原點 $(0,0,0)$ 進行旋轉,之後,我們對旋轉之後的版本進行一個平移,移至屏幕的右下角。記住,實際的轉換操作順序應該反過來讀,雖然在代碼層面,我們先平移再旋轉,但實際上轉換是先應用旋轉再應用平移的。要理解所有這些轉換的合併,以及它們如何對物件進行轉換,是一件不簡單的事情。試著動手像這樣實驗這些變換,你很快就能掌握其中的要領。
如果做得不錯的話,你應該得到以下結果:
你現在完成了!一個平移後的箱子,隨著時間的行走,它不斷旋轉。現在,你應該明白為什麼說矩陣在圖形領域是如此的有用。我們可以定義無數的轉換然後合併它們,使成為一個矩陣,然後我們可以反覆地去使用它。如此將轉換使用在著色器當中幫助我們節省了重新定義頂點數據的精力,也節省了很多處理時間,因為由此我們不用反覆向著色器發送頂點數據(這非常的耗時間);我們要做的全部的事情就是更新轉換對應的統一變量。
如果你沒有得到正確的結果,或者你遇到了什麼其它的困難,看看這裡的源代碼,以及這份更新後的著色器類。
下一章,我們將討論如何使用矩陣來為我們的頂點定義各種座標空間(座標系)。這是踏入 3D 圖形的第一步!