第九章：开始 • 座標系統

發布時間：2025-06-11 閱讀時間：41 分鐘

在上一章，我們知道了如何使用矩陣作為武器，來實現對頂點的轉換。對於那些你希望被渲染在屏幕上的頂點，OpenGL 要求它們在跑完 shader 代碼之後，全部落在標準設備座標（NDC）空間。也就是說，每個頂點的 x、y、z 座標都應該落在 -1.0 到 +1.0 之間；對於此範圍之外的點，它們將無法被看到。我們通常的做法是，在一個範圍（或者空間）裡指定一個座標系，這個座標系由我們自己來決定，然後在頂點著色器裡將頂點座標轉換為標準設備座標。接著這些 NDC 被交給光珊，以將它們轉換為屏幕 2D 座標/像素。

將座標轉換為 NDC 通常是一步一步來完成的，其中，我們會將一個物件的頂點轉換到若干個座標系統，最終才是 NDC 系統。經過若干個座標系統轉換的好處是，某些操作/計算只在特定座標系統才更容易，我們馬上就可以看到。一共有 5 個不同的座標系統，它們對我們來說是重要的：

• 本地空間（或者，物件空間）：Local Space
• 世界空間：World Space
• 視圖空間（或者，視覺空間）：View Space
• 裁剪空間： Clip Space
• 屏幕空間：Screen Space

這些都是頂點在最終變成片段（fragments）之前所經歷的不同轉換階段。

到目前，你或許對這些空間或者座標系實際是什麼感到有些困惑。那麼我們會站在一個更高的層次來對它們進行解釋，先展示一張全局圖，然後說一下每一個空間所代表的含義。

全局圖

要將座標從一個空間轉換到下一個空間，我們將使用到幾個轉換矩陣，其中最重要的是 Model、View 和 Projection 矩陣。我們的頂點座標首先處在本地空間，作為本地座標存儲，然後會被處理成世界座標、視圖座標、裁剪座標，以及最終的屏幕座標。下面這張圖顯示了整個處理流程以及每個轉換都做了什麼：

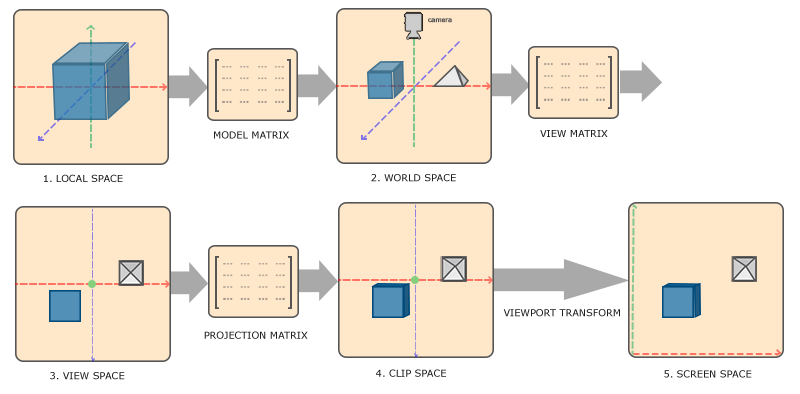
1. 本地座標就是你物件相對它本地原點的座標，它們是物件所在座標的開始。
2. 接下來的一步是將本地座標轉換為世界空間座標，這些座標相對一個更大的世界。它們的位置相對世界一個中心，很多其它物件也會相對整個世界中心被放進來。
3. 接下來，我們將世界座標轉換為視圖空間座標，其中，每一個座標都是從相機或者觀察者的眼睛出發被看到的。
4. 在座標放進視圖空間之後，我們還需要將它們投射成裁剪座標。裁剪座標會被處理為 -1.0 到 1.0 之間，它們決定了那些頂點最終會被顯示在屏幕上。如果使用了透視投射，裁剪空間便有了透視效果。
5. 最後，我們將裁剪座標轉換為屏幕座標，這裡我們採取了一個被稱為視窗轉換的處理，它將座標從 -1.0 到 1.0 轉換到 glViewport 定義的座標範圍。最終的座標被發送到光珊，被變為片元（fragments）

你或許對這些空間的用途有一些了解。至於我們為什麼要將頂點依次放入這些空間，那是因為，在特定座標系統中進行一些操作會顯得更容易。比如，當我們要修改物件本身時，在本地空間進行是非常合適的；當基於其它物件進行一些計算的時候，放在世界座標系下進行會更合理；如此等等。如果我們願意，我們也可以定義唯一的一個轉換矩陣，它包含了從本地空間到裁剪空間的全部轉換，然而，這樣會讓我們失去靈活性。

我們現在來對每一個座標系進行詳細的討論。

本地空間（Local Space）

本地空間是相對物件而言的座標空間，也就是物件一開始所處的空間。設想一下，你使用一個模型軟件（像 Blender）創建了一個方塊。這個方塊的原點可能是在位置 $(0,0,0)$，雖然在最終應用運行的時候，它可能出現在一個不同的位置。可能你創建的全部模型都使用 $(0,0,0)$ 作為起始位置。模型中的全部頂點因此在本地空間：它們（頂點）對於物件全是局部的。

對於我們在使用的箱子，它的頂點座標都在 -0.5 到 0.5 之間，0.0 是它的原點。它們因此都是本地座標，或者叫做局部座標。

世界空間（World space）

如果我們將所有的物件導入到應用，它們可能會被放置在世界的中心位置 $(0,0,0)$，並相互重疊，這並不是我們想要的結果。我們需要為每一個物件定義一個位置，這個位置相對於整個世界座標系。世界空間裡的座標就如它的名字那樣：你的所有頂點座標都相對一個（遊戲）世界。這正是你想將你的物件變換到的那個座標系統，物件分散其中（最好以一種真實的方式呈現）。你的物件的座標從本地轉換到世界空間，這一步由 Model Matrix 完成。

Model Matrix 是一種轉換矩陣，它對你的物件進行平移、縮放以及旋轉，從而放置到世界的某個位置，以它需要的朝向。考慮一個房子，我們對它進行縮小轉換（它在本地看上去太大了），然後平移至郊外的一個鎮子上，並在沿著 Y 軸稍稍向左旋轉一點，這樣它和其它相鄰的房子排列的更和諧。你可能想到了上一章出現的那個矩陣，它將箱子擺到整個場景一個位置上，那個矩陣也是一種 Model Matrix。我們將箱子的本地座標轉換到場景/世界的某個位置。

視圖空間（View space）

視圖空間就是人們常常提及的 OpenGL 相機（它有時候也會被稱為相機空間或者眼睛空間）。視圖空間（View Space）是將物體的世界空間座標轉換為相對於使用者視角前方的座標系之後所形成的空間。它因此也就是從相機的位置觀察時產生的空間。這通常是透過平移與旋轉的組合來實現的，目的是將場景中的某些物件轉換到攝影機前方的位置。這些轉換組合通常保存在視圖矩陣裡，它將世界座標轉到視圖空間。下一章我們會全面地討論如何創建這樣一個視圖矩陣，以模擬一個相機。

裁剪空間（Clip space）

在每一個頂點著色器運行的結尾，OpenGL 期望座標落在某一個範圍之內，範圍之外的座標將被裁剪掉。爾裁剪掉的座標將被丟棄，這樣，餘下的座標將作為片段呈現在你的屏幕上。這也就是裁剪空間之所以稱為裁剪空間的原因。

由於直接把所有可見物體的座標限制在 -1.0 到 1.0 之間並不直觀，我們通常會在一個自定義的座標系中工作，最後再將座標轉換成 OpenGL 所要求的 NDC（Normalized Device Coordinates）範圍。

要將頂點座標從視圖空間轉到裁剪空間，我們定義一個所謂的投影矩陣，它將每個緯度的座標範圍指定在 -1000 到 1000 之間。透視矩陣然後會將這個範圍裡的座標轉換為標準設備座標 $(-1.0, 1.0)$ （並非直接完成，其中包含一步，叫做透視除法）。範圍之外的座標將不會被映射到 -1.0 到 1.0，也就是被裁剪掉了。這個範圍我們也會在透視矩陣裡指定，座標 $(1250, 500, 750)$ 將不會出現，因為 其 x 座標超出範圍，轉換出來的值將超過 NDC 的 1.0，因此被裁剪掉。

請注意，如果一個圖元（例如三角形）只有部分超出裁剪體積，OpenGL 會將該三角形重新構建為一個或多個三角形，使其完全落在裁剪範圍內。

投影矩陣創建出來的視圖盒子被稱為視椎，落在此視椎裡的每一個座標都最終會呈現在用戶的屏幕裡。整個將特定範圍裡的座標轉為 NDC （可以很容易被映射到 2D 視圖空間）的處理被稱為投影，因為投影矩陣將 3D 座標投射為方便映射 2D 的標準設備座標。

一旦全部的頂點被轉換到裁剪空間，最後一步——透視除法——會被執行，其中我們將 x、y、z 分量分別除以向量的齊次座標 w 分量。透視除法用於對 4D 裁剪空間座標轉換為 3D 標準設備座標。這一步在頂點著色器的最後自動被執行。

這個階段之後，最終的座標會被映射到屏幕座標（使用 glViewport 的設置），並轉變為片元（fragments）。

這種負責將視圖空間座標轉為裁剪空間座標的投影矩陣通常有兩種形式，各自都會定義自己的視椎。我們可以創建一個正交投影矩陣（orthographic projection matrix）或者一個透視投影矩陣（perspective projection matrix）。

正交投影（Orthographic projection）

正交投影定義了一個立方體形的椎體盒子，它指定了裁剪空間，其中盒子之外的頂點都將被裁剪掉。當創建一個正交投影矩陣的時候，我們指定視椎的寬、高和長度。所有落在視椎內的座標經過轉換最終都會在 NDC 範圍裡，因而不會被裁剪。這個椎體看上去像一個箱子：

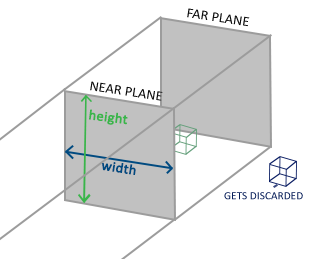
通過指定寬、高，near 和 far 平面，椎體確定可見的座標。任何座標，如果它在 near 平面之前，它會被裁剪掉，對於 far 平面之後的座標，情況也一樣。正交椎體直接將椎體裡的座標映射為標準化設備座標，爾不需要任何其它處理，因為它不涉及 w 分量；如果 w 分量保持為 1.0，透視除法不會改變座標值。

要創建一個正交投射矩陣，我們使用 glm 內置的函數 glm::ortho：

glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);

前面兩個參數指定了椎體左右兩邊的座標；第三、第四個參數指定了視椎的下方和上方。使用這個 4 個參數，我們定義出了 near 和 far 平面的大小，第五和第六個參數指明了 near 和 far 平面到視點之間的距離。這種投影矩陣將全部在這些 x、y、z 範圍內的座標轉換為標準設備座標。

正交投影矩陣直接將座標映射到 2D 平面，也就是你的屏幕。但是現實中，直接投影會產生一種不真實感，因為投影沒有將透視效果考慮在內。這就是透視投影矩陣為我們做的修正：

透視投影（Perspective projection）

如果你曾經很喜歡圖形，真實的生活一定讓你注意到遠處的物體裡距離越遠，顯得就越小。這種奇怪的效應，我們稱之為透視。透視很容易被觀察到，當我們看向無限遠處的高速路或者鐵軌時，就如下面這張圖所示：

如你所見，由於透視效果，線條會在足夠遠的距離處重合。這正好就是透視投影嘗試模擬的地方，它通過一個透視投影矩陣實現。投影矩陣將給定的椎體映射到裁剪空間，但是同時也對每個頂點座標的 w 值進行一種操作，就是如果頂點座標離視點越遠，w 的值越高。一旦座標被轉到裁剪空間，它們將會落在 -w 和 w 之間（之外的內容全部被裁剪掉）。經過最後一個頂點著色器輸出後，OpenGL 要求可見座標必須落入 -1.0 到 1.0 數值範圍，因此一旦座標在裁剪空間，透視除法會被應用到裁剪空間座標：

\text{out} = \begin{pmatrix}
x/{w} \\
y/{w} \\
z/{w}
\end{pmatrix}

頂點座標的每一個分量除以 w 分量後，頂點位置裡視點越遠，頂點座標越小。這也是 w 分量十分重要的另一個原因，因為它能幫助我們做透視投影。最終的座標於是在標準化設備座標空間。如果你對 orthographic 和 perspective 投射矩陣的計算（對數學不太畏懼 😂）感興趣，並想弄懂它們，我推薦 Songho 的這篇絕佳的文章。

使用 GLM，一個透視投影矩陣可以這樣被創建出來：

glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);

glm::perspective 所做的事情是創建一個大的椎體，用於定義可見空間，任何椎體之外的東西最後也都將在裁剪空間之外，因而被裁剪掉。透視椎體被可視化為一個非均勻的盒子，其中盒子中的每一個座標都將被映射為裁剪空間裡的一個點。用一張圖來說明透視椎體圖下：

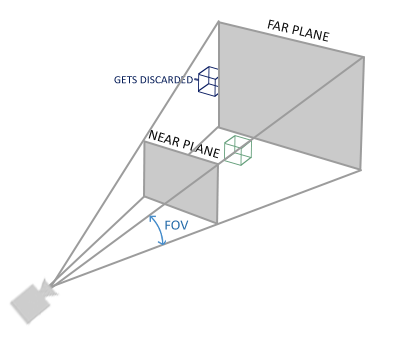
第一個參數定義 fov 的值，它的意思是 field of view，描述 viewspace 有多大。為了真實性，它通常被設置為 45 度，但是為了一些更加 doom-style 的效果，你可以將它設置得更高一些。第二個參數設置了 aspect ratio，使用視窗的寬度除以它的高度可以得到這個值。 第三個和第四個參數設置了椎體的 near 和 far 平面。我們通常將 near 距離設置為 0.1，並將 far 距離設置為 100.0。處於 near 和 far 平面之間，並且在椎體內部的全部頂點將會被渲染。

當你將透視矩陣的 near 值設置太高（比如 10.0），OpenGL 會裁剪掉太靠近相機（0.0 到 10.0 之間）的座標，這將導致你注意到一種效果，你可能曾在視頻遊戲裡見到過，當過於靠近一些物體時，你能夠從視覺上穿透它們。

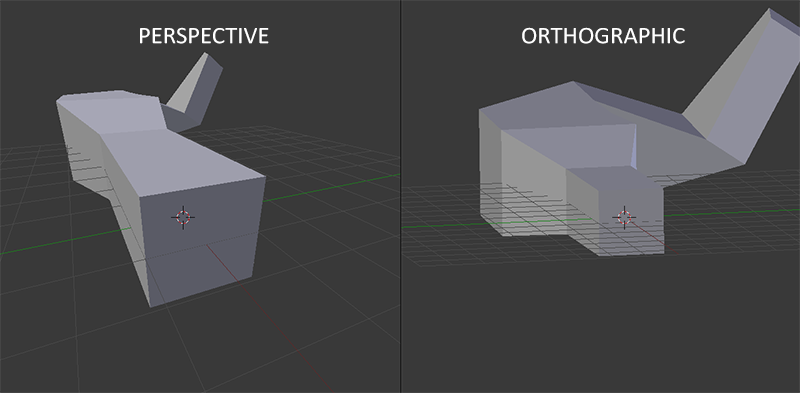
當使用正交投影，每一個頂點座標直接被映射到裁剪空間，不需要巧妙的透視除法（它仍然進行了透視除法，但是 w 分量沒有經過處理，因為 w 始終是 1，因此沒有效果）。由於正交投影不使用透視，遠處的物體不會變小，這產生了一種奇怪的效果。鑒於此，正交投影主要用於 2D 渲染，以及用於一些建築或者工程類應用，這些應用不需要將頂點做透視變形。類似 Blender 這種用於處理 3D 建模的軟件，有時候也會使用正交投影，因為需要更精確地刻畫每一個物體的大小。以下你將看到 Blender 下這兩種投影的比較：

放在一起

我們為上述步驟分別創建了轉換矩陣：model、view 以及 projection 矩陣。頂點座標於是按照以下方式轉換為裁剪座標：

\vec{V}_{clip} = M_{projection} \cdot M_{view} \cdot M_{model} \cdot \vec{V}_{local}

注意，矩陣乘法的順序是反的（記住我們需要從右往左地去閱讀矩陣乘法）。在頂點著色器中，最終的頂點需要交給 gl_Position，OpenGL 會自動執行透視除法以及裁剪。

接下來呢?

經過頂點著色器輸出的頂點要求其座標在裁剪空間，我們剛剛使用一些轉換矩陣所做的事情正是要達到這個目的。OpenGL 接下來會對裁剪空間座標執行透視除法，將它們放入標準設備座標系。OpenGL 使用 glViewPort 的參數將 NDC 轉換為屏幕座標，每一個座標對應你屏幕上的一個點（在我們這裡是一個 800x600 的屏幕）。這個過程被稱為視窗轉換。

這是最難理解的部分，如果你依然沒有對這些空間準確理解，不必慌張。接下來你將看到我們可以實際如何使用這些座標空間，在接下來的章節裡也會有大量的例子呈現給你。

進入 3D

現在我們知道如何將 3D 座標轉換為 2D 座標，我們可以開始渲染真正的 3D 物體，而不是我們此前演示的那種無趣的 2D 屏平面。

要在 3D 空間繪製物體，我們首先創建 model 矩陣。model 矩陣包含了平移、縮放以及旋轉，我們用它來將物體的全部頂點轉換到全局世界空間。讓我們將我們的平面沿著 x 軸稍稍旋轉一點，讓它看上去像是躺在地上。這裡 model 矩陣看上去是這樣的：

glm::mat4 model = glm::mat4(1.0f);
model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));

通過讓頂點座標與 model 矩陣相乘，我們將頂點座標轉化成世界座標。我們的平面因此微微倒向地面，這就是它在全局世界空間裡的呈現。

接下來，我們需要創建 view 矩陣。我們希望在場景裡稍稍向後退一點，這樣物件可以被看到（在世界空間，我們將 $(0,0,0)$ 設定為萬物的原點）。要圍繞場景移動，考慮以下表述：

• 將相機向後移動，和將整個場景向前移動是等效的。

這正是 view 矩陣所做的事情，我們會將整個場景反向地移動，來達到攝影機移動到指定位置的效果。由於我們需要向後移動，OpenGL 是一個遵循右手法則的系統，我們需要在 z 軸上移動。我們通過對場景沿著 z 軸的負方向平移達到這個目的。這樣可以給我們一種印象——我們在後退。

右手座標系統

按照慣例，OpenGL 是一個右手坐標系。這基本上表示正的 x 軸朝右，正的 y 軸朝上，而正的 z 軸朝後。你可以想像螢幕是三個坐標軸的中心，而正的 z 軸從螢幕穿出，朝向你。坐標軸繪製如下圖所示：

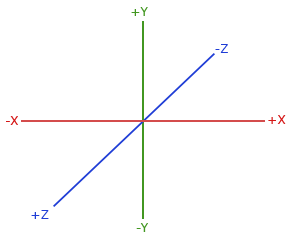
為了理解為什麼叫做右手坐標系，請這樣做：

• 伸出你的右手，沿著正的 y 軸方向舉起手。
• 讓你的拇指指向右邊。
• 讓你的食指指向上方。
• 然後將你的中指向下彎曲 90 度。

如果你做對了，你的拇指應該指向正的 x 軸，食指指向正的 y 軸，而中指指向正的 z 軸。如果你用左手做這個動作，你會發現 z 軸的方向是反的。這就是所謂的左手坐標系，DirectX 就常使用這種系統。請注意，在標準化裝置坐標（NDC）中，OpenGL 實際上使用的是左手坐標系（投影矩陣會改變慣用手系統）。

我們將在下一章裡詳細地討論如何移動場景。現在我們的 view 矩陣看起來這樣：

glm::mat4 view = glm::mat4(1.0f);
// note that we're translating the scene in the reverse direction of where we want to move
view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));

最後一件事，我們需要定義投影矩陣。我們希望為我們的場景使用透視投影，因此我們聲明一個透視矩陣，像這樣：

glm::mat4 projection;
projection = glm::perspective(glm::radians(45.0f), 800.0f / 600.0f, 0.1f, 100.0f);

現在，我們創建了轉換矩陣，我們要將它們傳入到著色器中。首先讓我們在頂點著色器中將轉換矩陣聲明為 uniforms，並且讓它們和頂點座標相乘：

#version 330 core
layout (location = 0) in vec3 aPos;
...
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

void main()
{
    // note that we read the multiplication from right to left
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    ...
}

我們應該也將矩陣發送到 shader（通常會在每一幀做這個事情，因為矩陣經常改變）：

int modelLoc = glGetUniformLocation(ourShader.ID, "model");
glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
... // same for View Matrix and Projection Matrix

現在我們的頂點座標通過 model、view 和 projection 被轉換，最終的物體將：

• 向地面傾倒
• 離我們稍遠
• 有了透視感（越遠的頂點，顯示上越小）

讓我們來檢驗一下最終的結果是否確實如我們所願：

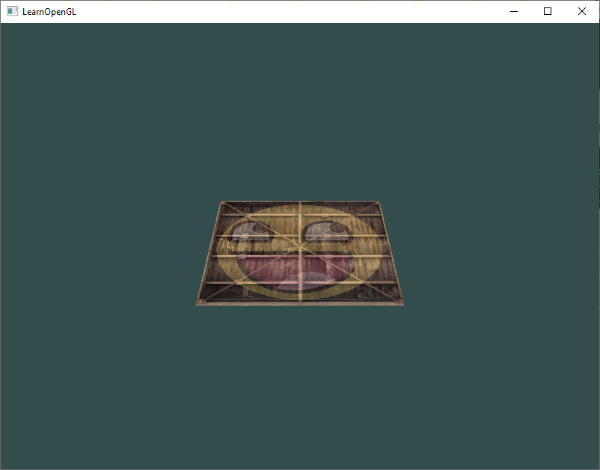
當然，它看上去很 3D 了，一個在可想像的地面上休息的“平面”。如果你沒有獲得一致的結果，將你的代碼和完整的源代碼做一番比對。

更加 3D

目前為止，我們處理的只是一個 2D 的平面，雖然我們將它放入 3D 空間了，讓我們來一點更有挑戰的路徑，將我們的 2D 平面 擴展為 3D 的方塊。要渲染一個方塊，我們需要一共 36 個頂點（6 個面 * 2 個三角形 * 3 个頂點）。36 個頂點算起來還不少，你可以從這裡獲取它們。

為了有趣一點，我們讓這個方塊隨著時間旋轉起來：

model = glm::rotate(model, (float)glfwGetTime() * glm::radians(50.0f), glm::vec3(0.5f, 1.0f, 0.0f));

然後，我們將使用 glDrawArrays（因為我們沒有指定索引）來繪製這個方塊，但是目前我們使用 36 個頂點。

glDrawArrays(GL_TRIANGLES, 0, 36);

你應該對以下動畫有些熟悉：

它確實有點像方塊，但是哪裡怪怪的。方塊的有些面畫在了另一些面的上方。這是因為 OpenGL 是逐個三角形、逐個片元繪製的，如此就會覆蓋一些已經畫好的像素。由於 OpenGL 不確保三角形的繪製次序（在一次 draw call 內），有些三角形繪製在彼此的上方，儘管其中一個明顯應該繪製在另一個的前面（立鏡頭更近）。

好消息是，OpenGL 保存了“深度”信息，它們被保存在一個叫 z-buffer 的緩衝對象裡，這允許 OpenGL 判斷什麼時候需要覆蓋像素、什麼時候不需要。使用 z-buffer，我們可以配置 OpenGL 以進行深度測試。

z-buffer

OpenGL 保存了全部的深度信息，放在 z-buffer 當中，也被稱為深度緩衝。GLFW 自動為你創建了這個 buffer（就像它有一個顏色緩衝區，用來儲存輸出影像的顏色一樣）。深度針對每一個片元（作為片元的 z 值）存儲，任何時候片元需要輸出它的顏色，OpenGL 會比較 z-buffer 中的深度值。如果當前的片元在其它片元之後，該片元會被丟棄，否則寫入。這個過程被稱為深度測試，OpenGL 會自動執行這部分。

然而，如果我們像確保 OpenGL 執行了深度測試，我們首先需要告訴 OpenGL 我們需要開啟深度測試；它默認是關閉的。我們可以使用 glEnable 開啟深度測試。glEnable 和 glDisable 函數允許我們開啟/關閉 OpenGL 的某些功能。指定的功能於是被打開/關閉，直到再此調用了它對功能進行了關閉/打開操作。現在，我們唷開啟深度測試，要開啟的是 GL_DEPTH_TEST：

glEnable(GL_DEPTH_TEST);

由於我們使用了深度緩衝（depth buffer），我們也希望在每一幀之前清除深度緩衝（否則，之前的深度信息會保留在 buffer 裡）。就像清理顏色 buffer 一樣，我們可以清理深度 buffer，這裡需要用到元位標記 DEPTH_BUFFER_BIT，調用的函數是 glClear：

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

讓我們重新運行程序，看 OpenGL 是否執行了深度測試：

太好了！正確地使用了深度測試之後，一個完整的、上了紋理的方塊現在隨著時間旋轉。你可以參考一下源代碼。

更多的方塊！

現在假設，我們希望在屏幕上顯示 10 個這樣的方塊。每一個方塊和此前我繪製的一樣，除了它們出現在世界的位置以及帶有的旋轉角不同之外。方塊的圖形佈局我們已經定義過的，因此在渲染更多方塊的時候，我們不必修改緩衝或者屬性（attributes）。唯一需要我們修改的是，每一個方塊的 model 矩陣，我們用它來將方塊轉換至世界空間。

首先，讓我們為每一個方塊定義平移向量，它指定了方塊的世界位置。我們將定義 10 個方塊的位置，放在 glm::vec3 數組當中：

glm::vec3 cubePositions[] = {
    glm::vec3( 0.0f,  0.0f,  0.0f),
    glm::vec3( 2.0f,  5.0f, -15.0f),
    glm::vec3(-1.5f, -2.2f, -2.5f),
    glm::vec3(-3.8f, -2.0f, -12.3f),
    glm::vec3( 2.4f, -0.4f, -3.5f),
    glm::vec3(-1.7f,  3.0f, -7.5f),
    glm::vec3( 1.3f, -2.0f, -2.5f),
    glm::vec3( 1.5f,  2.0f, -2.5f),
    glm::vec3( 1.5f,  0.2f, -1.5f),
    glm::vec3(-1.3f,  1.0f, -1.5f)
};

現在，在渲染循環函數裡，我們需要調用 glDrawArrays 10 次，但是這次在發送 draw call 請求之前，我們要發送不同的 model 矩陣到頂點著色器。我們將在渲染循環裡創建一個小的循環，以使用不同的 model 矩陣對我們的物體渲染 10 次。注意，我們也需要分別為每一個箱子添加一點旋轉效果。

glBindVertexArray(VAO);
for(unsigned int i = 0; i < 10; i++)
{
    glm::mat4 model = glm::mat4(1.0f);
    model = glm::translate(model, cubePositions[i]);
    float angle = 20.0f * i;
    model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
    ourShader.setMat4("model", model);

    glDrawArrays(GL_TRIANGLES, 0, 36);
}

這段代碼做的事情是，每一個新的方塊被繪製的時，更新它的 model 矩陣，如此執行一共 10 次。現在我們應該可以看到世界中放入了 10 個隨機旋轉的方塊：

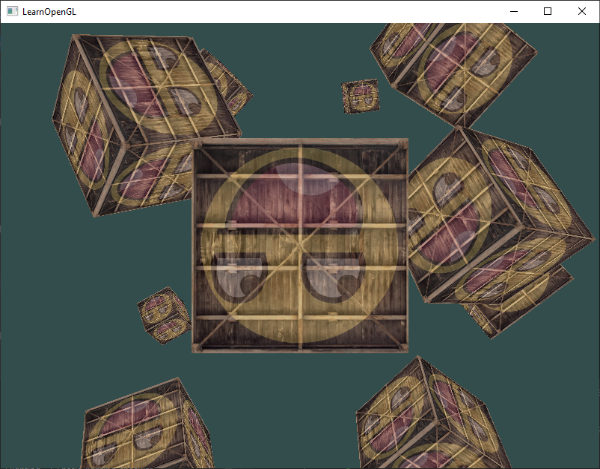
完美！看上去，我們的箱子找到了幾個志同道合的朋友 😄。如果你遇到了困難，看看是否可以將你的代碼與源代碼對照一下。

上一章：开始 • 轉換 下一章：开始 • 相機

章節

• 一：介绍
• 二：开始 • 认识 OpenGL
• 三：开始 • 创建一个窗口
• 四：开始 • Hello, 窗口
• 五：开始 • Hello, 三角形
• 六：开始 • 著色器
• 七：开始 • 紋理
• 八：开始 • 轉換
• 九：开始 • 座標系統
• 十：开始 • 相機