说明
翻译自费曼物理学讲义,空时一章,翻译了前三部分,后边关于四维矢量的讲解未翻译。
目录
- 几何
- 间隔
- 分区
几何
相对性理论向我们表明了,不同坐标系下位置与时间之间的关系,并非如我们所直观预期的那样。非常重要的一点是,我们必须深刻地明白,洛伦兹变换对于位置和时间暗含着的那种关联,因此我们要细致地考察一下这个问题。
对于静止观测系统下的位置和时间的测量,与以速度u相对其运行的“飞船系统”下的对应位置和时间的测量,洛伦兹变换的方程如下:
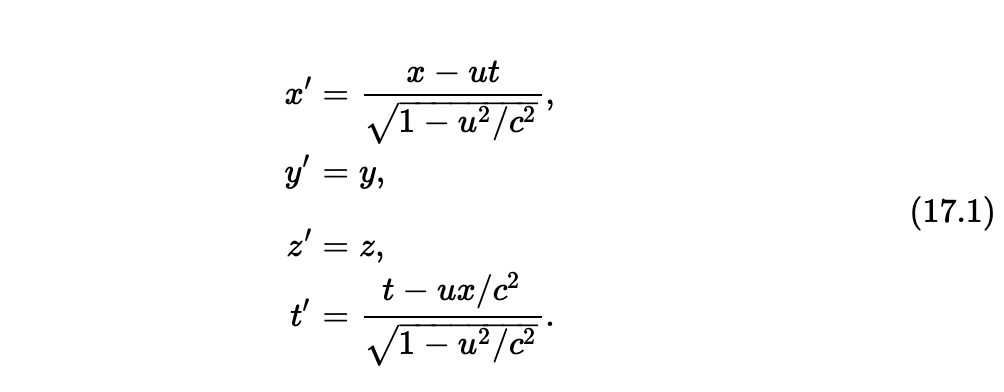
让我们将之与旋转变换比较一番,旋转变换也是和两个观测系统里的测量有关,其中之一即是:
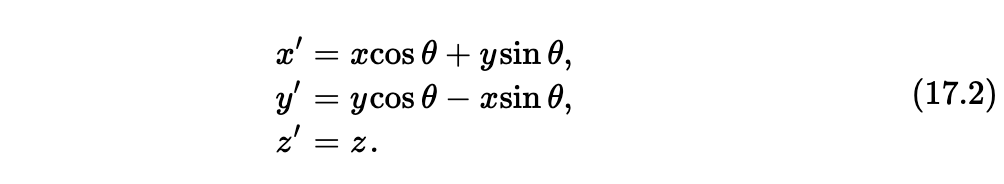
在此特例,Moe 和 Joe 正在基于各自的轴线进行测量,两个轴线 x- 和 x'- 之间的夹角是θ。对于每一方面,我们注意到“基本”量都被两个“非基本”量混合:新的x'是 x 和 y的混淆,而新的y'也是 x 和 y 的混合。
类比总是有用的:当我们看着一个物体的时候,有一个明显可见的东西,可以称之为“可见宽度”,另一个或许可以称为“可见深度”。但是这两个概念,“宽度”和“深度”,都不是这个物体的基础属性,因为当我们移到一旁,或者从不同的角度看这个物体的时候,我们会得到不同的“宽度”和“深度”,并且我们或许还可以发现某种算式,其中以角度和旧的观测量为函,以计算得新的观测量。方程 17.2 就是这类算式。有人可能会说,一个给定的深度是全部深度和全部宽度的混合。如果物体不发生移动,且我们总是从同一个位置去观察它,那么这些问题都是无关紧要的——我们总是看到了真的“宽度”和“高度”,并且,它们也将呈现出不同的量,这是因为它们有些是通过某种视角(subtended optical angle )呈现,另外的借助了某种调焦眼( focusing of the eyes )或者干脆使用肉眼使之呈现; 它们看起来可能会非常的不同,但永远不会被弄混乱。那是因为我们可以围绕着物体进行观察,继而意识到了深度和宽度其实是,一定程度上讲是,同一个物体的不同方面。
那我们是否能以同样的方式看待洛伦兹变换呢?洛伦兹变换同样存在对测量值的混合——位置和时间。空间测量和时间测量之间的差异产生了一个新的空间量。换句话,在另一个人看来,一个人所测量的空间量会混入一点时间量。我们的类比允许我们产生这样的一个想法:我们正观察着的物体的“真实”物理量,一定意义上来说(粗略地讲),比它看起来的“宽”和“深”要大一些,因为这取决于我们如何看它。当我们移至一个新的位置,我们的大脑会立刻计算物体的大小,但是在快速移动的过程中,我们无法立刻计算出物体的实际大小;因为我们没有近光速移动的经验,以认同时间和空间同性的事实。我们就如同自始至终停留在一个位置,因之总是看到物体的一个侧面——“宽”,而无法显著地移动我们的脑袋。如果我们可以,我们现在就能明白,我们可以看到其他人的时间侧面——我们能看到“之后”,一点点吧。
因此我们将尝试在一个新的世界看看我们身边的物体,那里的时间和空间混在一起,它和我们在通常空间世界中感知物体的方式一样真实,且可以从不同的方向去观察。我们将考虑这样的物体,它占据了一些空间,同时还延续了一定长度的时间,它在一种新的世界中,占有一个“空时块”(blob),我们可以从不同的角度、在或快或慢地移动中观察这个“空时块”。这个新的世界,由占据一个位置且延续一定长度的时间的几何实体,以此方式存在于其中,就被称为“空时”。在空时中,一个给定的点(x,y,z,t)被称为一个事件。想象一下,我们在水平方向画出 x 的系列位置,y 和 z 在另外两个方向上,二者相交以“合适的角度”,并且以“合适的角度”相对于你面向的这张纸(屏幕),时间线合乎垂直方向。如此,那么一个运动的粒子,在这张图上看起来会是怎样的呢?如果这个粒子是静止的,那它有某个 x,随着时间的向前推进,x 还是这个 x,时间继续推进,x 依旧是这个 x,也就是 x 一贯是这个 x;因此它的路径就是一条和 t 轴平行的线(fig 17-1 a)。另一方面,如果它向外滑动,那么随着时间的推进,x 随之增加(Fig 17-1 b)。因此一个例子,比如,开始于快速向外滑动,继而缓缓停下,就会拥有这样的曲线(Fig 17-1 c)。换句话讲,一个稳定且不分裂的粒子在空时中就可以表达为一条线。一个发生分裂的粒子,在空时中就可以表达为一个分叉线,因为它将由分裂的位置开始,而变为两个其它的东西。
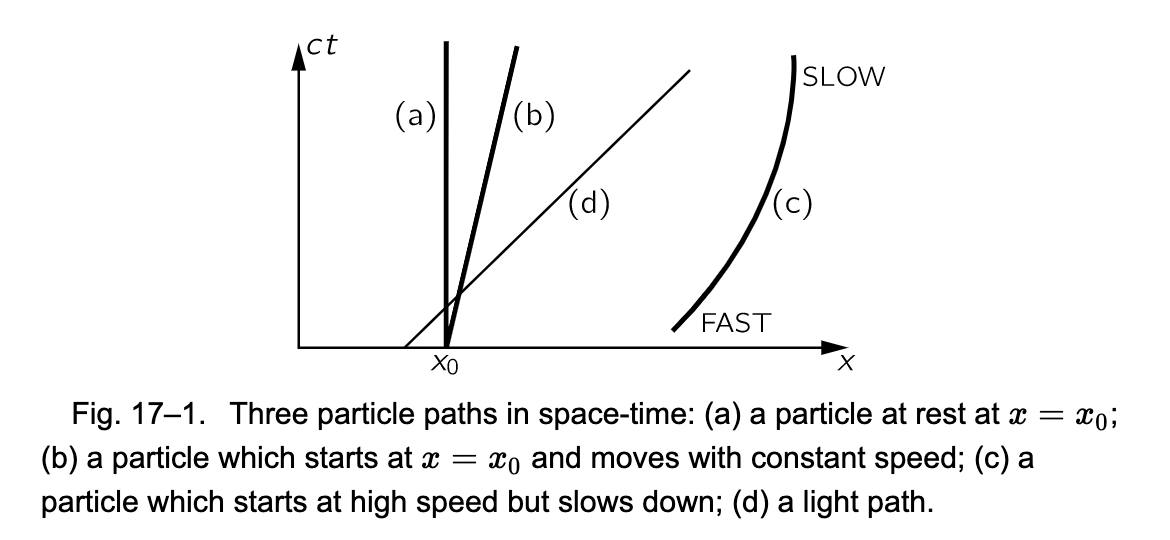
对于光来说怎样呢?光以速度 c 运行,因而会表达为一条恒定斜率的直线。
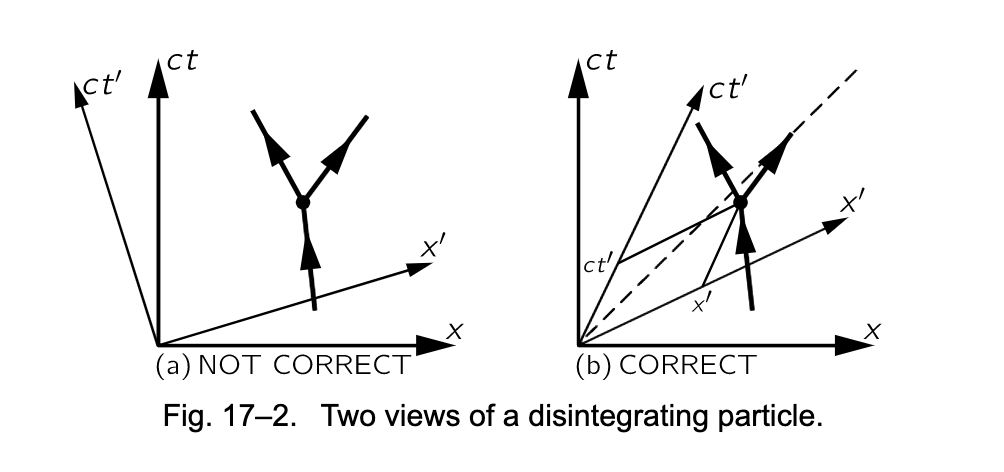
现在,根据我们这个新的想法,如果我们假定一个事件发生在一个粒子身上,比如说,它在空时中的某个点上突然一分为二,于是跟随出现了几个新的轨线,这个有趣的事件发生在特定的 x 坐标和特定的 t 坐标,我们可以期望的是,如果这有含义,我们可以分别取一对新的轴线来转换这些轨线,我们将指定一个新的 x 轴和一个新的 t 轴,如图 Fig 17-2 a。然而这是错误的!因为 Eq 17.1 和 Eq 17.2 实际上不是同样意义的数学变换。注意,比如,这里存在的数学符号差异,其中一个包含 cos 和 sin,但是另一个是代数量。(当然,并非说代数量一定不能写为 cos 和 sin,然而这二者是不行的)。继续,然而它们看起来很相似,我们即将看到,真的不可能将空时设想为一个真实的、类似通常意义上的几何形体,就因为所涉及的转换公式在数学符号上存在的差异。实际上,即使我们不去强调这点,结果是,一个移动中的人需要借助一系列的和光同斜率的轴线,同时借助一个向 x'-和 t'- 轴的投射来计算它的 x’ 和 t’ 坐标,见图 Fig 17-2 b。我们将不会处理这些几何计算,因为它对我们理解问题没什么帮助;使用方程很容易解决这些几何计算。
间隔
尽管空时几何并非欧几里得式的,但是二者在某些方面以奇怪的方式符合。如果这样的几何观是正确的,那么应该说存在基于位置和时间的某种函数,它无关于坐标(或者观测)系统的选择。举个例子,对于通常的旋转操作,如果我们选取两个点,简单起见,一个在原点上,另一个在其它地方,选择的两个(观测)系统的原点重合,那么明显的是它们到彼此的距离总是相同的数值。这就是跟测量系统选择无关的一个特性。它们的距离的平方等于 x2+y2+z2;那么空时系统如何呢?不难发现,如下算式总是恒等(变换无关的或者测量系统选择无关的)的:
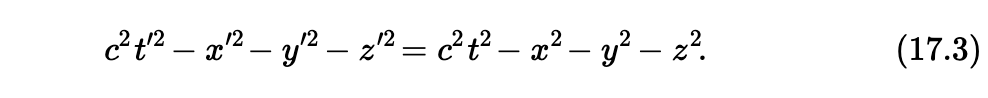
这个量因此就有些类似我们的通常说的距离,某种意义上,它是实数,它现在被称为两个空时点的之间的间隔(interval),其中一个在测量系统的原点。(当然实际上,它是 interval 的平方,就像我们的空间距离那样。)我们给了它一个不同的名字,因为它是针对一个不同的几何形体而言的,但是有趣的是,它们仅仅是正负相反,另外加进了 c 这个量。
我们抛开 c,如果我们想要得到一个 x 和 y 可以互换的空间,它会让事情不好理解。其中一个困扰就是,设想没有经验的某人来测量物体的大小,他以某个视角测量了宽度,然后用不同的方式测量深度,因此深度以feet为单位,而宽度以meter为单位。由此,它就给我们对于处理转换带来了巨大的麻烦,继而我们就看不到事物的简单和明白的一面,原因仅仅是我们对相同的物理量采取了不同的测量单位。现在 Eq 17.1 和 17.3 的本性告诉我们时间和空间是等效的,时间可以变为空间;它们应该采取相同的单位来测量。一秒的距离是什么?从 17.3 很容易看到它是什么。它是 3x108 米,光在真空运行 1 秒所产生的距离。换句话,如果我们以相同的单位测量距离和时间,比如以“秒”,那么我们这里距离的单位就是 3x108 米,如此我们的方程看上去就更加的简单。或者,我们也可以使得所有的量采用的单位都是米。那么一米是多久呢?时间上,一米就是光行走一米需要花的时间,也就是 1/3x10-8 秒,或者 3.3x 109 分之一秒。我们更希望将我们的所有方程都置于同一个单位系统下,它使得方程中的c = 1。如果时间和空间都使用同样的单位测量,那么方程就看上去非常简明,如下:
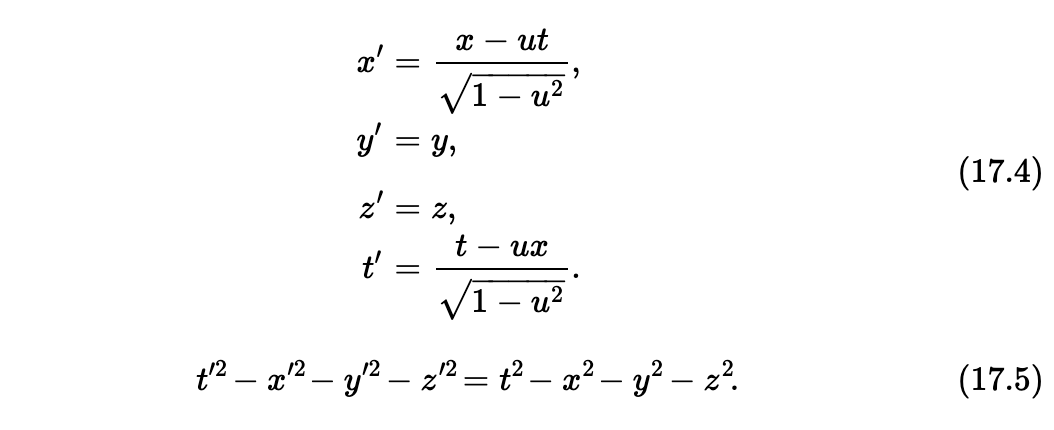
是否对此感到不确定和惊愕,认为这样由设置 c = 1 而得到的简化表达是存在问题的?刚好相反,它非但正确,事实上我们很容易记住这个没有 c 存在于其中的方程,且也很容易将 c 再加回来, by looking after the dimensions 🤔。例如,在 √1-u2 中,我们知道我们不能用 1 减去速度的平方,它蕴含的单位来自前面的数字 1,因此我们知道我们必须将 u 的平方除以 c 的平方,以使单位抵消,于是我们就可以做加减运算。
空时和通常的空间的差异,以及 interval 和距离的相关性是非常有趣的,根据 Eq 17.5, 如果我们考虑给定坐标系下的一个点的时间是 0,只有空间,那么 interval 的平方就是负数,我们将产生一个虚数 interval,它是一个负数的平方根。interval 理论上可以是实数也可以是虚数。 interval 的平方可以是正数,也可以是负数,不像距离,其平方只会以正数出现。当一个 interval 是一个虚数时,我们说两个点之间有一个 space-like (类空间)间隔,因为这个 interval 相较于时间上的片段更像是空间上的距离。另外一方面,如果两个物体在给定坐标系统的同一个位置,但是时间不同,那么时间的平方是正数,而距离是零,那么 interval 的平方就是正的;这被称为 time-like(类时间) 间隔。在我们的空时图中,因此可以这么说:在 45 度处,有两条线(实际上,在四维系统,它们是锥,被称为光锥 )和一些在此两条线上的点,都与系统原点间距为 0。光总是会以 0 间隔从给定点出发,如 Eq 17.5 所示。恰巧,我们于此也证明了:如果光以速度 c 穿行在一个系统中,它们也会以相同的 c 量运行于另一个系统。因为如果空时间隔在两个系统中相等,比如说都为“零”,那么说“光的传播速度是不变的”也就相当于说“其空时间隔(interval)是零”。
分区
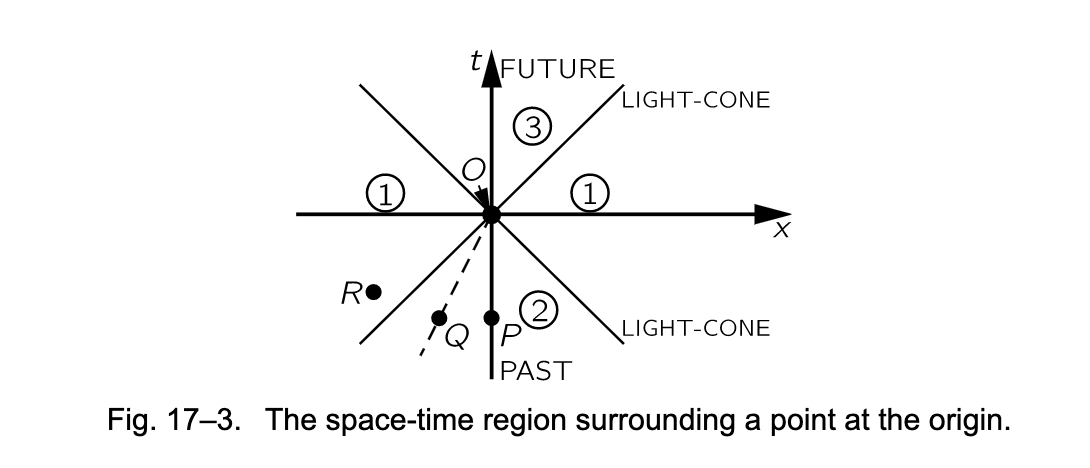
围绕一个给定的空时点,可以将空时划分为三个区域,上图所示。其中一个区域存在 space-like 间隔,另外两个存在 time-like 间隔。物理上说,围绕空时点的这三个区和该点有一个有意思的关系:一个物体或者一个信号可以以一个低于光速的速度,由区域 2 的某点出发到达事件 O。因此此区域(2)里的事件能够影响到 O,可以由过去对其施加一定的作用。实际上,当然了,一个位于 t-负半轴上的事件 P 确实在严格意义上就是 O 的过去。它就是空时点 O,只是时间上比较早。P 的时候所发生的事情对此时的 O 固然是存在影响的。(不幸的是,我们日常的生活就是如此)另一个物体 Q 可以以一个低于 c 的速度到达 O,因而如果这个物体在一个运行的飞船里的话,它将也会是同一个空时点的过去。也就是说,在另一个系统中,时间轴线可能都经过 O 和 Q。因此所有在区域 2 里的点都是 O 的过去了,任何在此发生的事情都会影响到 O。因此 2 区有时候被叫做 afttective past,或者 affecting past;它是全部能够影响到 O 的事件总和。
另一方面,区域 3 是能够受影响于 O 的点的总和,我们能够发射一颗子弹,以低于 c 的速度,击中某个东西。因此这是一个可以被我们影响的区域,我们称其为 affective future。现在看看其它区域(1),很有趣,我们既不能自 O 影响它们,也不能由它们来影响 O,因为没有什么能够比光速还快。当然,在空时点 R 处所发生的事情会稍晚影响到我们;也就是,如果“此刻”,太阳爆炸了,需要八分钟之后,我们才知道,我们不可能早于这个时间得知太阳的爆炸。
“此刻”的含义是一个难解的谜题,我们不能定义、不能影响,但是它能够稍后影响我们,或者说我们需要在足够早的某个时候做点什么才能影响到它。当我们看着 Alpha Centauri,我们看到的是四年之前的它;我们或许好奇什么是“现在”。“现在”意味着与我们所在的测量系统处于同一时刻。我们只能通过光看到从我们过去而来的 Alpha Centauri,早在四年之前的那个时候,我们无法知道它此时在做什么;需要再等四年的时间,我们才能知道它此刻在做什么。“现在” 的Alpha Centauri 是一个理念或者一个脑海里的概念;它不是某种可以被物理地定义的东西,因为我们必须等待它的到来以对其进行观察;我们甚至无法此刻,就在此刻就对“此刻”进行指定。此外,“现在”还取决于观测系统。比如,如果说 Alpha Centauri 正在移动,那里的一个观测者不会与我们这边的观测者对于观测的结果达成一致,因为他可能将他的观测系统的轴线旋转了一个角度,他的“现在”就因此会是一个不同的时间。我们已经讨论过这个事实,就是同时性并非单一的东西。
有些算命的人,或者身边的人,会扬言他们知道未来,也有许多的令人神往的故事,说有些人突然发现他们掌握了关于未来的知识。好吧,由此产生了许多的悖论,因为如果我们真的知道了什么即将发生,那么我们必然有能力想办法阻止它的发生,我们会采取一些对的行动,在对的时间开展这些行动,诸如此类。但是实际上没有哪个算命先生能够告诉我们“当下”正在发生什么!没有任何人能够告诉我们现在究竟发生着什么,哪怕在我们有限的距离之内的事情,因为“此刻”的它们是不可观测的。我们或许要问自己这样的问题,也是我想留给大家去尝试回答的问题:
假设,我们突然能够知道区域 1 中的某些事情,会产生什么悖论?
